Expand (2x-y 2)^3 247104-Expand (2x-y+3z)^2

Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, itUse the binomial theorem to find the 18th term in the binomial expansion of `(2xysqrt(2))^27` ` ` 3) Find the 69th number in the 72nd row (n=72) of Pascal's triangle 4) Refer to the photoPre Calculus Equations Inequalities Simultaneous Equations System of Inequalities Polynomials Rationales Coordinate Geometry Complex Numbers Polar/Cartesian Functions Arithmetic & Comp Conic Sections Trigonometry Calculus

Ex 2 5 4 Expand Each Of The Following Using Suitable

Expand (2x-y+3z)^2

Expand (2x-y+3z)^2-Thank you taylorexpansion Share Cite Follow edited Mar 9 '16 at 024 Michael Hardy 255k 28 28 gold badges 253 253 silver badges 542 542 bronze badgesClick here👆to get an answer to your question ️ Expand each of the following, using suitable identities(i) (x 2y 4z)^2 (ii) (2x y z)^2 (iii) ( 2x 3y 2z)^2 (iv) (3a 7b c)^2 (v) ( 2x 5y 3z)^2 (vi) 1/4a 1/2b 1 ^2

Ials Expand Each Of The Following Using Suitable Identities Scholr

 Answer 6x3y6 Stepbystep explanation (2xy2)3 3*2x3*y3*2 =6x3y6 laminiaduo7 and 25 more users found this answer helpful heart outlined Thanks 13Expand following, using suitable identities (–2x 5y – 3z)^2 CBSE CBSE (English Medium) Class 9 Textbook Solutions 50 Important Solutions 1 Question Bank Solutions 7801 Concept Notes & Videos 2 Syllabus Advertisement Remove all ads Expand following, using suitable identities (–2x 5y – 3z)^2 MathematicsExpand each of the following, using suitable identities (2x y z)^2 > 8th > Maths > Squares and Square Roots > Finding Square of a Number > Expand each of the followin

What is the coefficient of {eq}x^2 y^3 {/eq} in the expansion of {eq}(2x y)^5? So the expansion becomes (x2y)^7 = 1x^7y^07x^6(2y)^121x^5(2y)^235x^4(2y)^335x^3(2y)^421x^2(2y)^57x^1(2y)^61x^0(2y)^7 Cleaned up a bit, it becomes (x2y)^7 = x^714x^6y84x^5y^2280x^4y^3560x^3y^4672x^2y^5448x^1y^6128y^7 In this finalIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive

$3x^{1/2}y O(x/y)^3$ I think Taylor expansion would do it The thing is, I don't really know around what point I should do it Could anyone help here?You can put this solution on YOUR website!3rd term (2x y)^13;

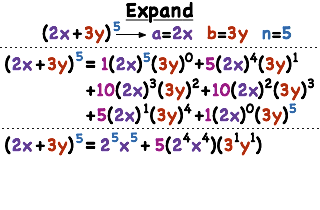
How Do You Expand A Power Of A Binomial Sum Using The Binomial Theorem Virtual Nerd Can Help

Files Schudio Com Brgs Files Edexcel Transistion From Gcse To A Level Files 1 Pdf

 Find an answer to your question expand by using identity (2x y z)^2 shubham5616 shubham5616 Math Secondary School answered Expand by using identity (2x y z)^2 2 See answers gaurav13c gaurav13c MarkAsBrainliest MarkAsBrainliest We know that,All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}2y3=0 x 2 − 2 x y 2 2 y − 3 = 0 This equation is in standard form ax^ {2}bxc=0Algebra Expand using the Binomial Theorem (2xy)^3 (2x y)3 ( 2 x − y) 3 Use the binomial expansion theorem to find each term The binomial theorem states (a b)n = n ∑ k = 0nCk ⋅ (an kbk) ( a b) n = n ∑ k = 0 n C k ⋅ ( a n − k b k) 3 ∑ k = 0 3!

A Quick And Efficient Way To Expand Binomials Ppt Download

Expand And Simplify Binomial Squares 2x 3y 2 Youtube

A commonly misunderstood topic in precalculus is the expansion of binomials In this video we take a look at what the terminology means, make sense of theA 2 B 5 C 40 D 80 E it does not existX3 Substituting n = 3 and x for 2x ⇒ (2x 1)3 = 1 (3 ⋅ 2x) 3 ⋅ 2 2!

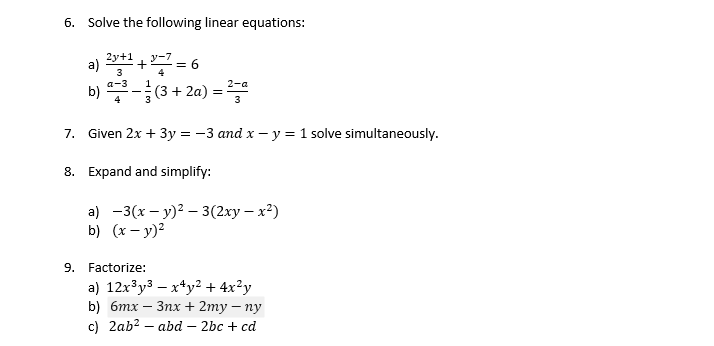
6 Solve The Following Linear Equations A 2y 1 3 Chegg Com

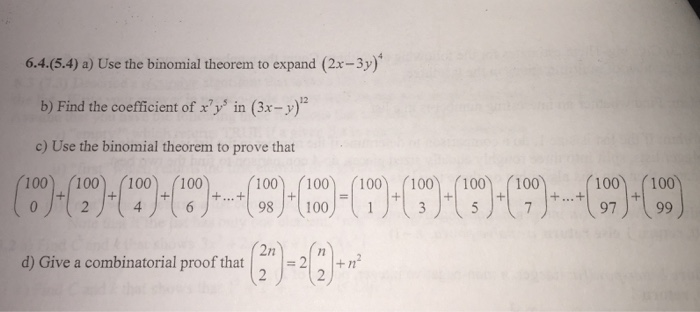
Use The Binomial Theorem To Expand 2x 3y 4 Find Chegg Com

Expandcalculator Expand (2x y)(3x^{2} 2xy 5y^{2}) he Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how SymbolabExpand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3Expandcalculator Expand (2xy)(3x4y) pt Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the

Ppt Algebra Expressions Powerpoint Presentation Free Download Id

Expand 2x Y 2 3 Novocom Top

Expand using the binomial theorem (2x 2y) 4 To expand (A B) n by the binomial theorem Start out with the 1st term, which is 1A n B 0 then 1 Multiply the numerical coefficient by the exponent of A, 2 Divide that by the number of term 3 Write that number down to start the next term 4 Beside that write A with an exponent that is 1 lessAlgebra Expand using the Binomial Theorem (2xy)^2 (2x − y)2 ( 2 x y) 2 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n ⁡ n C k ⋅ ( a n k b k) 2 ∑ k=0 2!Expression is (2x y 3z) 2 Formula used (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca Calculation (2x y 3z) 2 ⇒ (2x) 2 (y) 2 (3z) 2 2(2x)(y) 2(y)(3z) 2(3z)(2x) ⇒ 4x 2 y 2 9z 2 4xy 6yz 12xz Download Question With Solution PDF ››

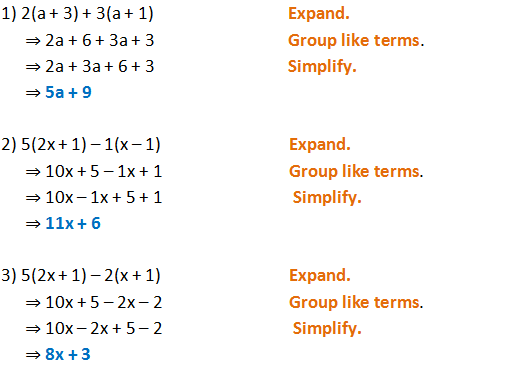
Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths

Solution Find The Term Involving X 2 In The Expansion Of X 3

Utilize the Binomial Expansion Calculator and enter your input term in the input field ie, $(2xy)^3$ & press the calculate button to get the result ie, $8x^3 12x^2y 6xy^2 y^3$ along with a detailed solution in a fraction of seconds Ex (x1)^2 (or) (x7)^7 (or) (x3)^4Expand each of the following, using suitable identities ( 2x 3y 2z)^2 > 8th > Maths > Squares and Square Roots > Finding Square of a Number{/eq} Binomial theorem Usually, we use normal multiplication to expand a

Solhj6i1bzqddm

11 1p Fnd The Value Of X2y222 See How To Solve It At Qanda

 Explanation The binomial theorem states that for any binomial (a b)n, the general expansion is given by (a b)n = twonCr ×an−r × br, where r is in ascending powers from 0 to n and n is in descending powers from n to 0 = two6C0(2x)6( −y)0 two6C1(2x)5( −y)1 two6C2(2x)4( −y)2 two6C3(2x)3( − y)3 two6C4(2x)2( − y)4 two6C5(2x)1( − y)5 two6C6(2x)0( − y)6Middle term (3x 2y)^6Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Find 2x Y 3z 4x2 Y2 9z2 2xy 3yz 6xz Studyrankersonline

Ex 2 5 4 Expand Each Of The Following Using Suitable

2 x = 3 − y Divide both sides by 2 Divide both sides by 2 \frac {2x} {2}=\frac {3y} {2} 2 2 x = 2 3 − y Dividing by 2 undoes the multiplication by 2 Dividing by 2 undoes the multiplication by 2 x=\frac {3y} {2} x = 2 3 − y8th term (2x y^2)^7; Find an answer to your question (2xyz)² expand using suitable identity deep255 deep255 Math Primary School answered • expert verified (2xyz)² expand using suitable identity 2 See answers DaIncredible DaIncredible Hey friend, Here is the answer you were looking for Hope this helps!!!!

Expand The Following 2x Y 3 Brainly In

Extra Practice

Expand 3 (2x3) 3(2x 3) 3 ( 2 x 3) Apply the distributive property 3(2x)3⋅ 3 3 ( 2 x) 3 ⋅ 3 Multiply Tap for more steps Multiply 2 2 by 3 3 6 x 3 ⋅ 3 6 x 3 ⋅ 3 Multiply 3 3 by 3 3⋅ (2x)2 3 ⋅ 2 ⋅ 1 3!Click here👆to get an answer to your question ️ Expand ( 2x 5y 3z )^2 using suitable identities

Expand I 2x 3y 2 Ii 3x 4y 2 Iii Brainly In

Expand 2x Y 2 3 Please Give The Answer Please Brainly In

 Ex 25, 4 Expand each of the following, using suitable identities (x 2y 4z)2 (x 2y 4z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = x , bQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions, combining several fractions into one and 8x^3 12x^2y 6xy^2 y^3 In general, for (ab)^k, the expansion is C(k,0)a^kb^0C(k,1)a^(k−1)b^1C(k,2)a^(k−2)b^2C(k,k−1)a^1b^(k−1)C(k,k)a^0b^k Note that, for example, C(4,0)=C(4,4)=1,C(4,1)=C(4,3)=4,C(4,2)=6 and Pascal's triangle gives a diagram representing binomial coefficients, namely 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 15 6

Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube

Expand Each Of The Following Using Suitable Identities X 2y 4z 2 2x Y Z 2 2x 3y 2z 2 Youtube

⋅ (2x)3 k ⋅ ( y)k What is the coefficient of x^2y^3 in the expansion of (2xy)^5 1 See answer percypercy168otvzio is waiting for your help Add your answer and earn points DelcieRiveria DelcieRiveria Answer The coefficient of x²y³ is 40 Stepbystep explanation The binomial expansion is defined asSee the answer 15)Expand Show transcribed image text Best Answer 100% (1 rating) Previous question Next question Transcribed Image Text from this Question Expand (2xy)3 Get more help from Chegg Solve it with our precalculus problem solver and calculator

Expand 2x 3y 5 Youtube

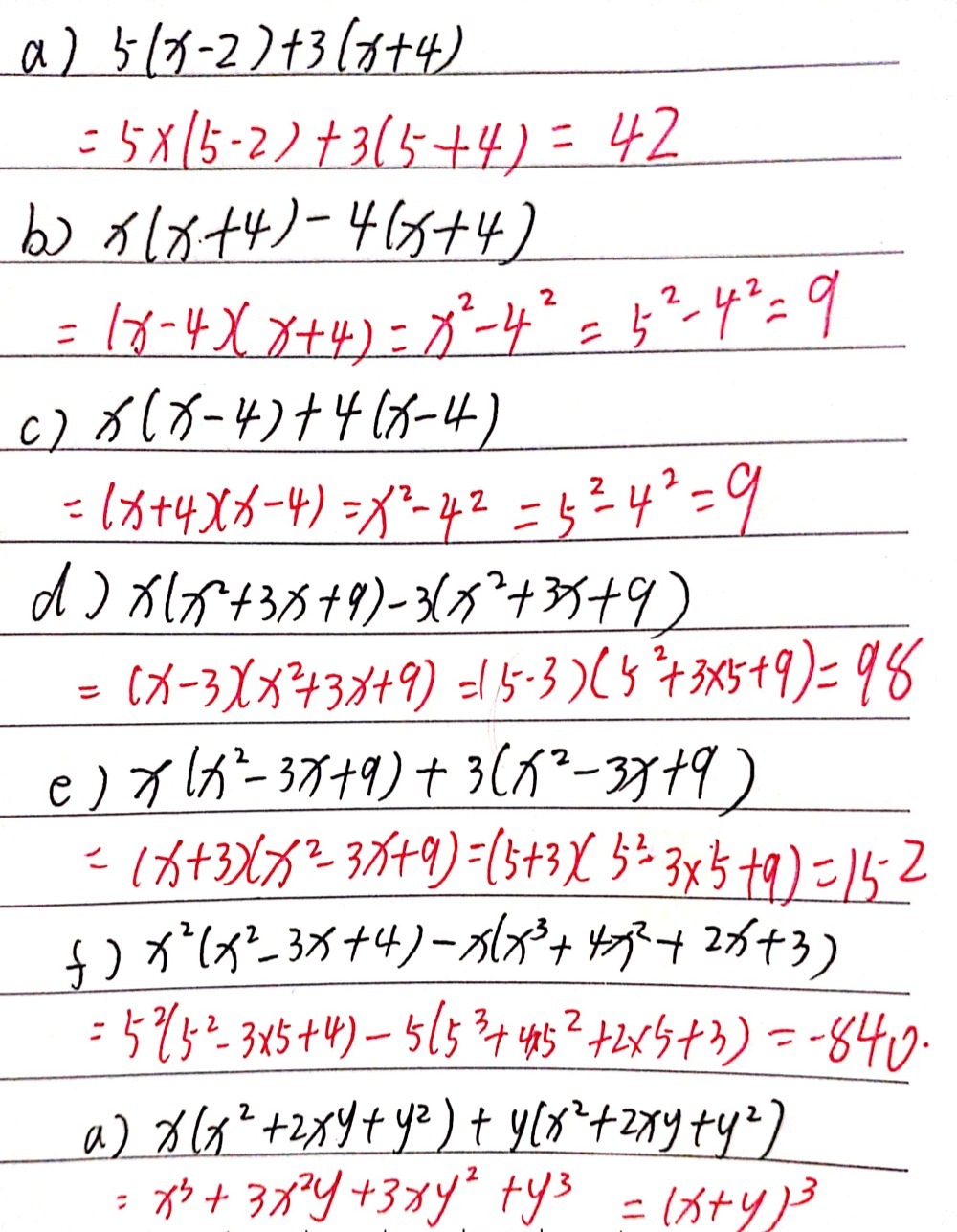
8 Expand The Parts Of Each Expression And Simpl Gauthmath

1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 15 6 1 Looking at the row that starts with 1,6, etc, we can see that this row has the numbers 1, 6, 15, , 15, 6, and 1 These numbers will be the coefficients of our expansion So to expand , simply followExpand (2x3y^2)^3 using pascals triangle Get the answers you need, now!⋅ (2x)3 = 1 6x 12x2 8x3 Method 2

Expand 2x 3y By Using Suitable Identity Brainly In

Q Tbn And9gcrdpn Ulimhqvv2g Cotaoqtmrx Bqjjfjii62kxva Usqp Cau

 what is the coefficient of x^2y^3 in the expansion of (2xy)^5?⋅(2x)2−k ⋅(−y)k ∑ k = 0 2 ⁡ 32x^5 80x^4y 80x^3y^2 40x^2y^3 10xy^4 y^5 For n=5, the binomial expansion of (ab)^5 given in the 6th row of Pascal triangle is a^5 5a^4b 10a^3b^210a^2b^35ab^4 b^5 Now to expand the given binomial, plug in a=2x, b=y to get the desired value It would be 32x^5 80x^4y 80x^3y^2 40x^2y^3 10xy^4 y^5

Expand The Following 1 A 2b2 2 3x 2y2 3 2x Y3 Gauthmath

Algebra Expansion And Factorisation Pdf Free Download

Expandcalculator Expand 2(x y) 3(x y) en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how SymbolabExpand (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Multiply by Add andBinomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Notice that the powers are descending in x and ascending in yAlthough FOILing is one way to solve these problems, there is a much easier way

How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Steps for Solving Linear Equation 2xy=2 2 x − y = 2 Add y to both sides Add y to both sides 2x=2y 2 x = 2 y The equation is in standard form The equation is in standard form5th term (x^2 y^3)^8;This calculator can be used to expand and simplify any polynomial expression

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

6 Binomial Theorem

Expand each binomial using the binomial theorem (3x y)^3 (2x 3y)^4 (a 2)^5 (2x 1)^4 (1 x)^7 (2a 3b)^6 (2/3x 2)^5 (3/4m 2/3k)^5 (a^1/2 3b^2)^4 (x/y 2/z)^4 (2x/y 3/z)^6 Find the indicated term of each binomial expansion (x y)^9;6th term (4x 2y)^5; We must use our knowledge of the binomial expansion Method 1 We can use (x 1)n = 1 nx n(n − 1) 2!

Using Binomial Theorem Write Down The Expansions Of The Following 2x 3y 4

Expand 2x 3y 4 In The Copy Maths Binomial Theorem Meritnation Com

Question Expand (2xy)3 This problem has been solved!X2 n(n − 1)(n −2) 3!The expansion of (2xy)^3 is (2x)^3 (2x)^2*y (2x)*y^2 y^3 = 8x^3–4x^2 y 2xy^2 y^3

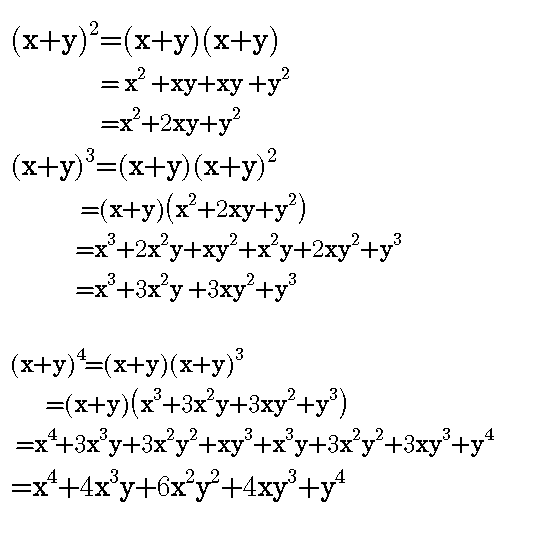
Worked Examples On Binomial Expansion Steemit

Algebra Expansion And Factorisation Pdf Free Download

$1,3,3,3,6,3,1,3,3,1$ in that order Now expand using everything to get $(2xy3z)^3=(2x)^3\mathbf3(2x)^2(y)\mathbf3(2x)^2(3z)\mathbf3(2x)(y)^2\mathbf6(2x)(y)(3z)\mathbf3(2x)(3z)^2(y)^3\mathbf3(y)^2(3z)\mathbf3(y)(3z)^2(3z)^3$The other tutor's answer is incorrect Use binomial expansion to expand the following (2x3y)4 The first term is (2x) the second term is (3y) The power is 4 so write " (2x) (3y)" one more than 4, that is, 5 times (2x) (3y) (2x) (3y) (2x) (3y) (2x) (3y) (2x) (3y) Give the first factor9th term (x^1/2 2)^10;

Expand The Following 2x Y 3 Brainly In

Expand 2x 3y Square Brainly In

Swap sides so that all variable terms are on the left hand side 2x3=y 2 x 3 = y Subtract 3 from both sides Subtract 3 from both sides 2x=y3 2 x = y − 3 Divide both sides by 2 Divide both sides by 2

Binomial Theorem Wikipedia

I Given A 2x 1x 2 3x 1x 2 B 5x Y 7x Y 2y 1 C 3a Gauthmath

Ex 2 5 4 Expand Each Of The Following Using Suitable

1 Expand The Following A 2x Y B X 3y F R 2y D 2a Scholr

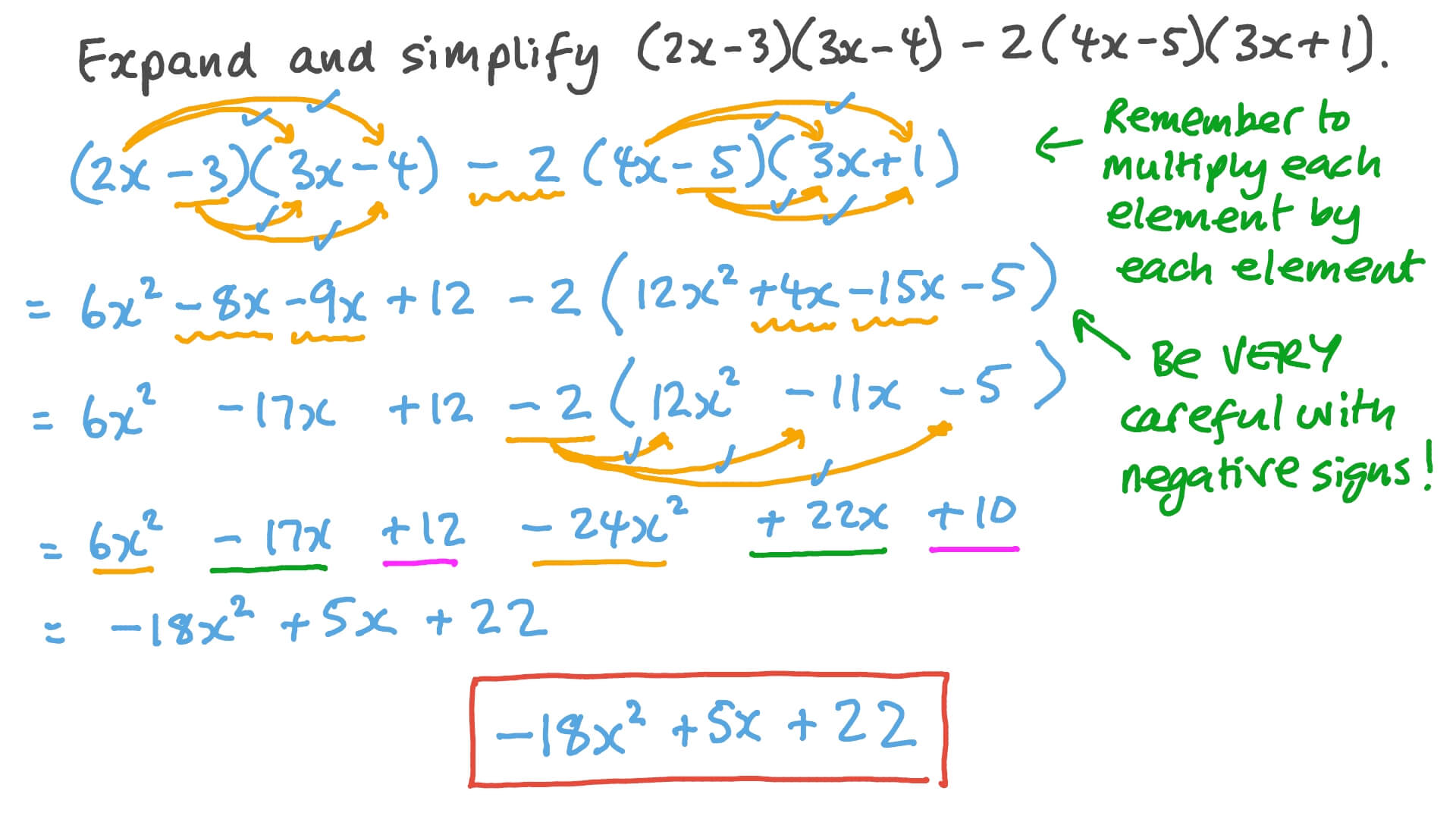
Question Video Expanding And Simplifying Algebraic Expressions Nagwa

Find The Coefficient Of X 10 In The Binomial Expansion Of 2x

How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic

Expand The Following Using Suitable Identities I 2x 3y 3 Ii X 2y 3z 2 Maths Polynomials Meritnation Com

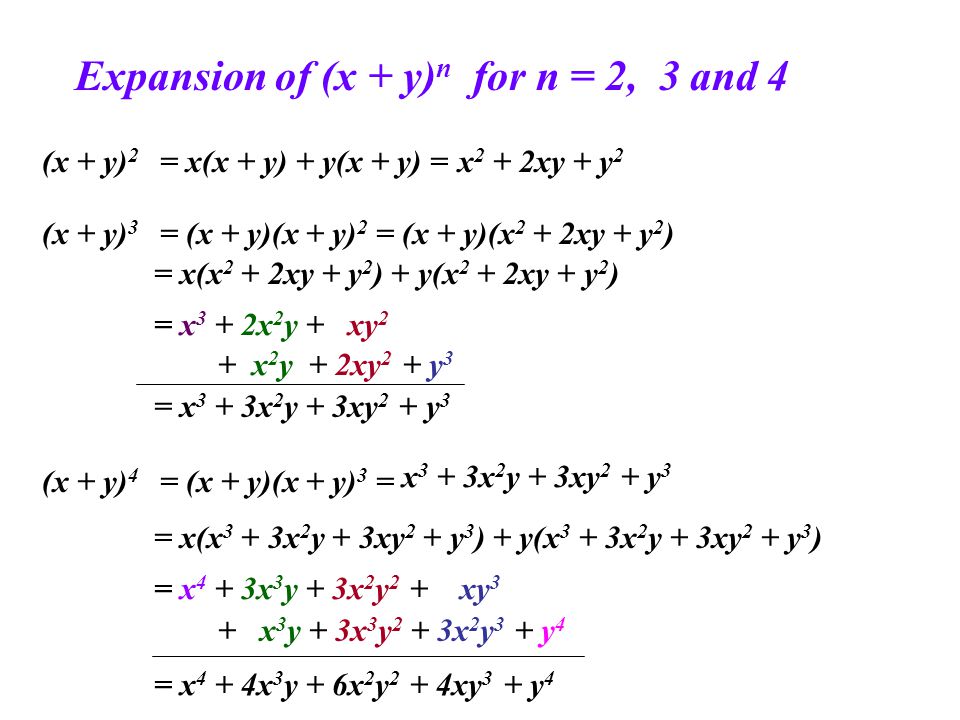
The Binomial Theorem 1 Objectives Pascal S Triangle Coefficient Of X Y N When N Is Large Notation Ncrncr Ppt Download

Expand 2x Y Z Please Answer Me Maths Polynomials Meritnation Com

Expand The Following 3 2x 2 3y 3 Brainly In

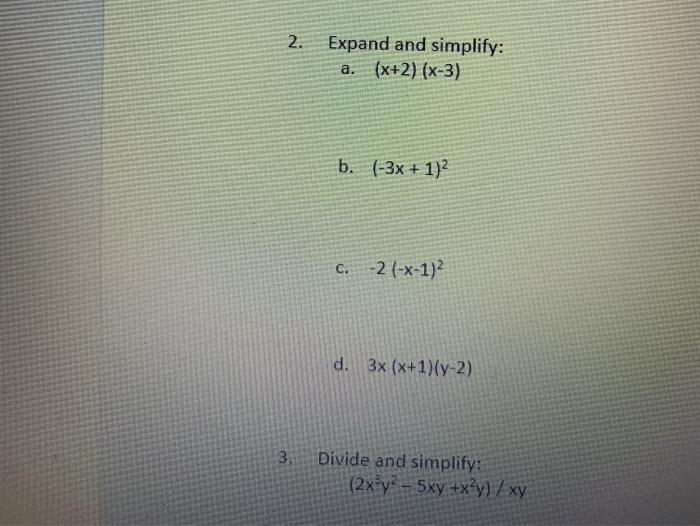
Solved 2 Expand And Simplify X 2 X 3 A B 3x 1 Chegg Com

Number Of Terms In Expansion Of Following I 2x 3y 9 Ii 2

Http Www2 Victoriacollege Edu Myosko Pascalstriangle Pdf

Using The Binomial Theorem Expand X 2y 3 3 2 3 Chegg Com

Section 8 5 The Binomial Theorem Ppt Download

Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z 2 Iii 2x 3y 2z 2 Iv 3a 7b

Expand 2x Y Z 3

6 Binomial Theorem

Expand Using The Identity A 2x 3y Z 2 Brainly In

How Can We Expand X Y 1 2 Youtube

Expand 2x 3 3 Maths Questions

Expand Each Of The Following Using Suitable Identities 2x Y Z 2

Ials Expand Each Of The Following Using Suitable Identities Scholr

How To Expand 2x Y 3 Quora

Expand 2x 3y Whole Square Maths Rational Numbers Meritnation Com

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

T Madas What Is 47 X 12 47

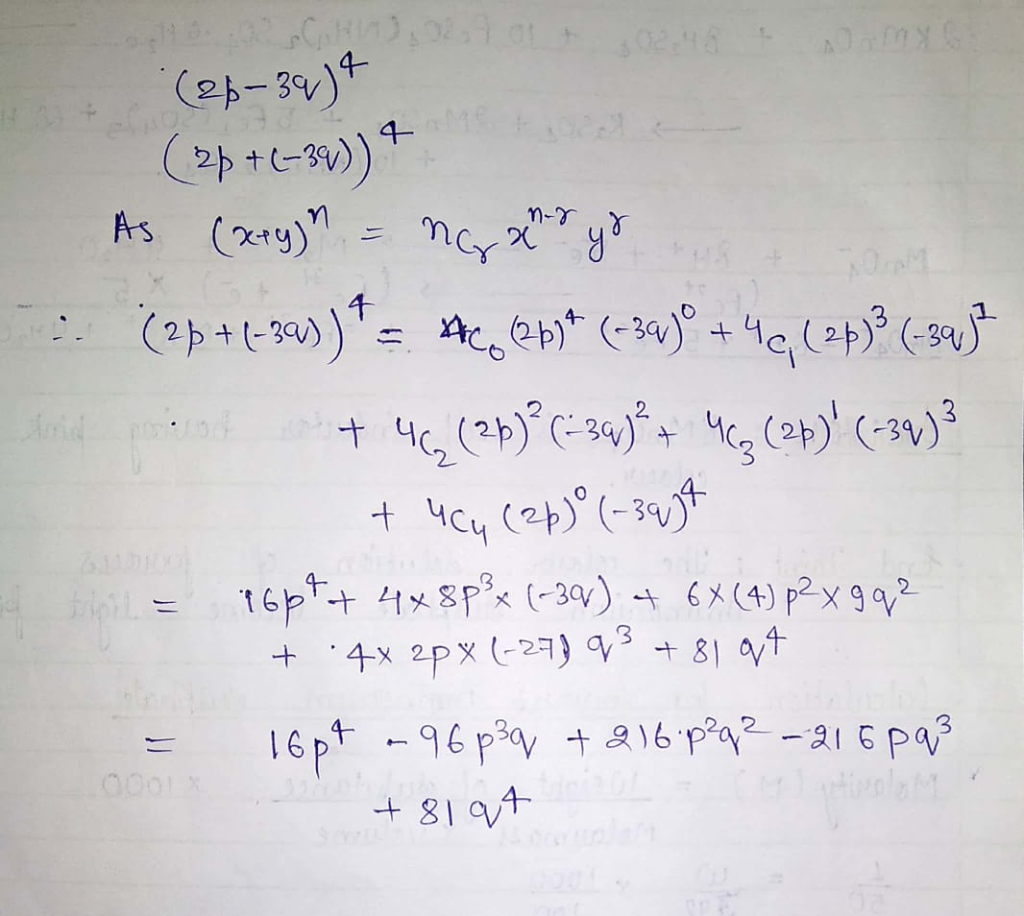
Solved 2 Expand Expression Using Binomial Theorem 2x 3y 3 B 3x 1 C 2p 34 D 3x H S Q

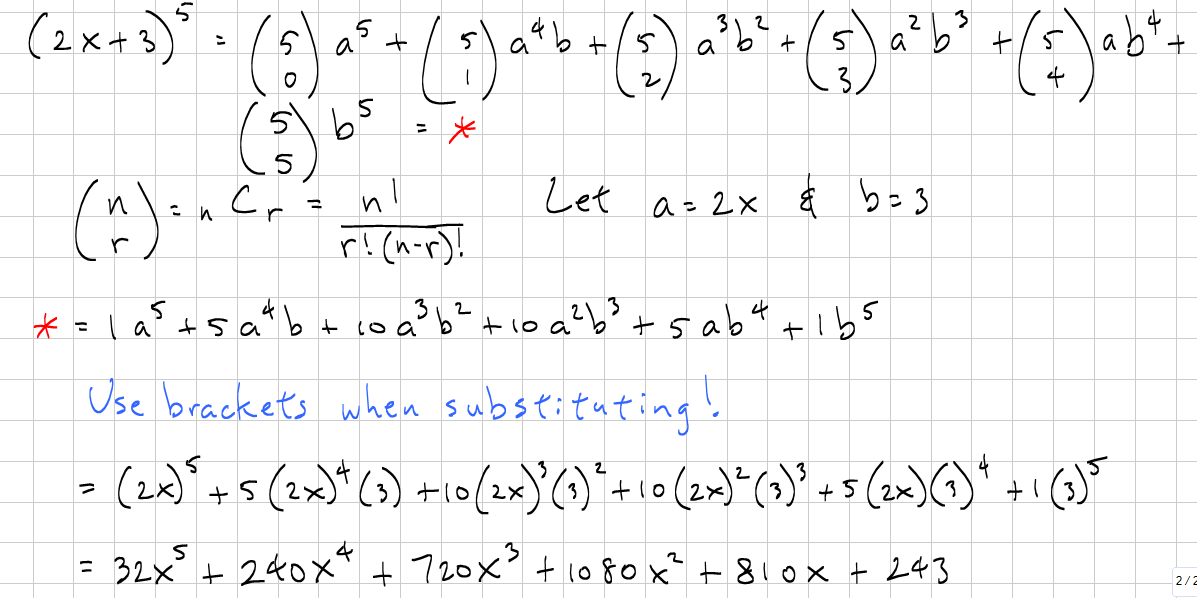
What Is The Binomial Expansion Of 2x 3 5 Socratic

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Using The Binomial Theorem College Algebra

Ex 2 5 4 Expand Each Of The Following Using Suitable

Answered C Expand G X As A 6x 1 6x 1 15 Bartleby

Preview Cambridge Igcse Mathematics Core And Extended Coursebook Revised Edition By Cambridge University Press Education Issuu

1

3 Expand And Simplify The Exp See How To Solve It At Qanda

1

Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download

Themathbooklets S2 N5 Expansion Of 2 Linear Expressions Add And Subtract Of Quadratic Expressions

How To Find The Constant Term In The Binomial Expansion Of 3x 1 2x 6 Quora

Ex 8 1 3 Expand 2x 3 6 Chapter 8 Class 11 Binomial

Polynomials 4 Expand Each Of The Following Using Suitable Identities 1 X 2y 4z

9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download

Expanding Factoring And Solving Sles Math173df

Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube

Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths

Expand This 2x 3y 3 Brainly In

Factorials To Binomial Theorem

Quiz Questions A Expand And Simplify 3x 5 2x 4 B Simplify 3x 2 5x 6x 2 2x 4 C Simplify 4x 2 Y 3 2 3 2 Y 2 2 Ppt Powerpoint

Q Tbn And9gcs2zs2yfches1lr N5klpkw0xqulrzmkaw3kumfnpmy Afpiwp Usqp Cau

Guysue Numbers Teaching Mathematics

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

Algebra Expressions Year 9 Note 1 Expressions We

Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9

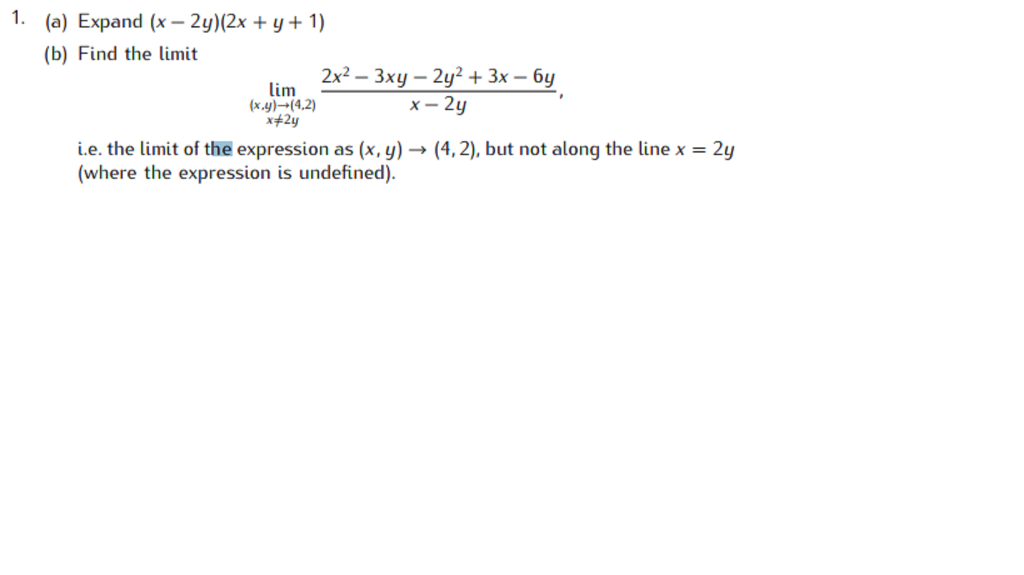
1 A Expand X 2y 2x Y 1 B Find The Limit Chegg Com

Expand 2x 3y 3 With Suitable Formula Brainly In

Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf

Expanding Binomials Video Polynomials Khan Academy

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials

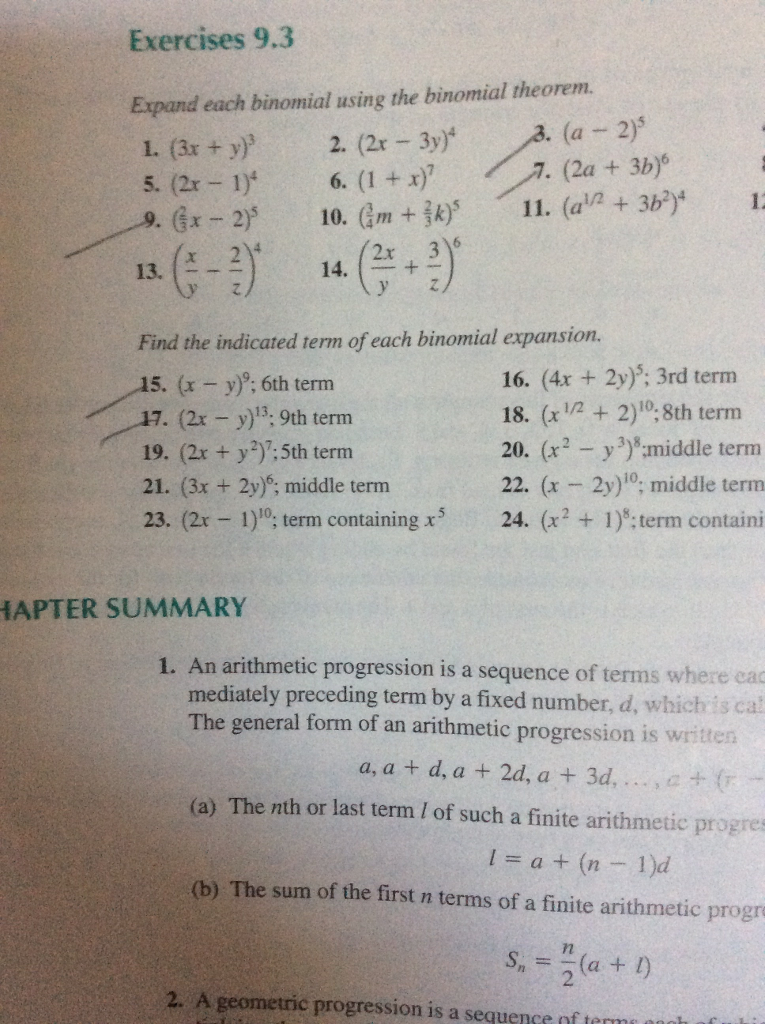
Expand Each Binomial Using The Binomial Theorem 3x Chegg Com

Year 12 C1 Binomial Theorem Task Expand The Following 1 X Y 1 2 X Y 2 3 X Y 3 4 X Y 4 What Do You Notice Powers Of X Start From Ppt Download

Expand Using Identity 2x 3y 3

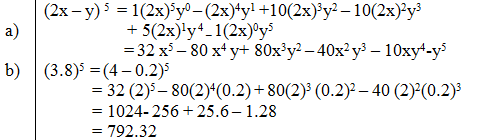
A Expand And Simplify The Binomial Expression 2x Y Sup 5 Sup B Use The First Four Terms Of The Expansion Above To Approximate The Value Of 3 8 Sup 5 Sup

Expand 2x 2 3 4 Your Answer If Y X 3 Find The Chegg Com

Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf

Expand 2x Y 2 2 Novocom Top

Expand Each Of The Following I 2x 5y 2 Ii X 3y 2 Iii

Incoming Term: expand (2x-y+2)^3, expand (2x-y+3z)^2,