Click here👆to get an answer to your question ️ Suppose the parabola (y k)^2 = 4(x h) with vertex A , passes through O = (0, 0) and L = (0, 2) Let D be an end point of the latus rectum Let the y axis intersect the axis of the parabola at P Then PDA is equal toY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yConic Sections Anatomy of a Parabola y = ax 2 bx c Û y = a(x – h) 2 k Û y = a(x – z 1)(x – z 2) Note x is squared and y is not for those that open up or down (The same function, but different forms of the equation) x = ay 2 by c Û x = a(y – h) 2 k Û x = a(y – z 1)(y – z 2) Note y is squared and x is not for those that open sideways
Illustrative Mathematics
Graphing a parabola of the form y = (x-h)2 + k calculator
Graphing a parabola of the form y = (x-h)2 + k calculator- y=mxb, and y=ax^2bxc are the GENERAL form of a line, and of a parabola They are easy to use for finding y values, and more convenient if using matrices AxBy=C, and y=a (xh)^2k are the STANDARD form for a line and for a parabola The numberline intercepts are easy to identify for the line, and the vertex is easy to identify for theFor sideways (horizontal) parabolas, the y part is squared The "vertex" form of a parabola with its vertex at (h, k) is regular y = a(x – h) 2 k
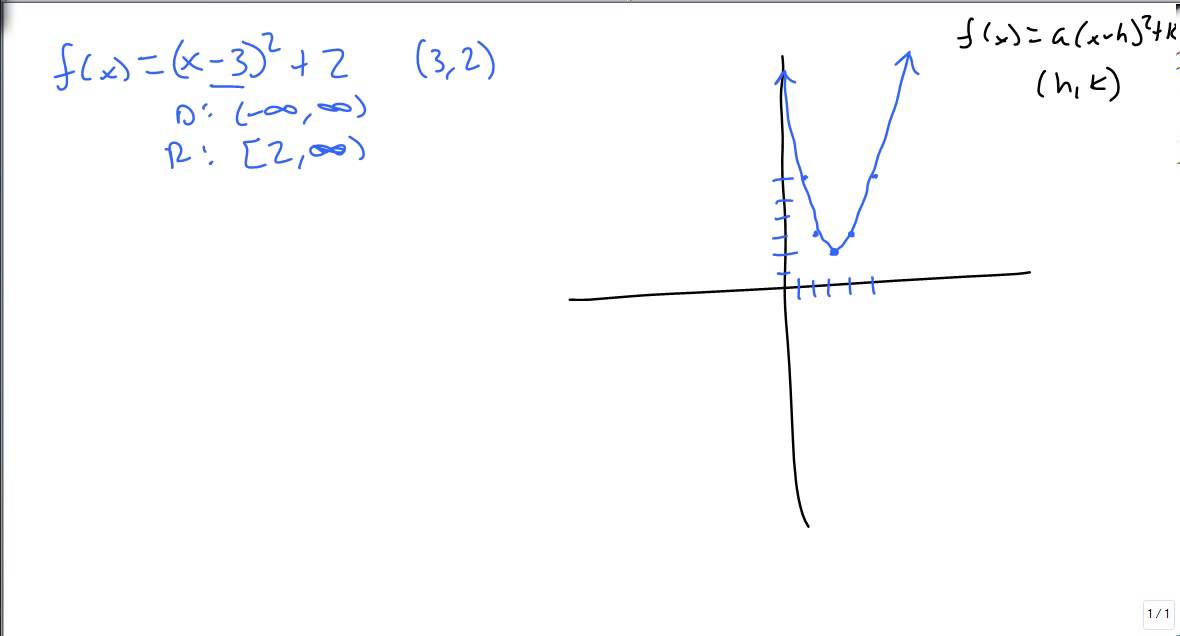



Graph By Transformations F X A X H 2 K Youtube
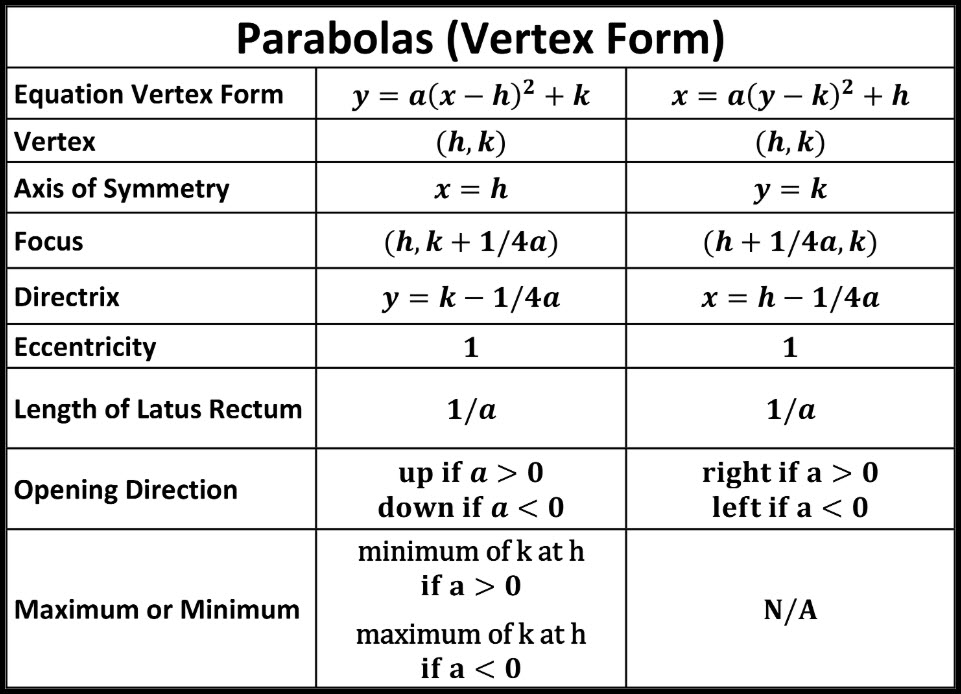
The line y=k1/4a represent in y=a(xh)^2k is Directrix Stepbystep explanation Directrix of a parabolaA directrix is a line which is perpendicular to the axis of symmetry of a parabola and it does not touch the parabola Also, for the standard equation of the parabola iePlug the values into the equation (x h) 2 = 4p(y k) so (x 4) 2 = 4(3)(y 6) Simplify giving (x 4\({\text{Parabolas (Alternative Vertex Form)}}\) \({\text{Equation Vertex Form}}\) \((xh)^2=4p(yk)\) \((yk)^2=4p(xh)\) \({\text{Focus}}\) \((h,kp)\) \((hp,k)\) \({\text{Directrix}}\) \(y=kp\) \(x=hp\) \({\text{Opening Direction}}\) \(\text{up if } p\gt0, \text{ down if } p \lt 0\)
Vertex form of a quadratic equation is y=a (xh) 2 k, where (h,k) is the vertex of the parabola Vertex form is useful, because it lets us pick out the vertex of a parabola really quickly just by looking at the equation!All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction ah^ {2}\left (2ax\right)hax^ {2}yk=0 a h 2 ( − 2 a x) h a x 2 − y k = 0Since the vertex of the parabola is already given, that is {eq}V(h,k) = V(1,2) {/eq}, we can substitute this value into the standard form of the equation of the parabola
Vertex (1,1) There are two methods to solve this Method 1 Converting to Vertex Form Vertex form can be represented as y=(xh)^2k where the point (h,k) is the vertex To do that, we should complete the square y=x^22x2 First, we should try to change the last number in a way so we can factor the entire thing => we should aim for y=x^22x1 to make it look like y=(x1)^2And the equation of the parabola is y = 1/4p (x h) 2 k Note that vertex will always be half way between the focus and the directrix The equation of the parabola in focus vertex form is (x h) 2 = 4p(y k) The vertex is at (h,k) giving us h = 4, k = 6;




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




What Is Vertex Form Example Get Education
Notice how there is a minus sign in front of 'h' in vertex formThe focus is located at (h, k p) In this example the focus is at (4, 3) so k p = 3 But k = 6 so p = 3 6 = 3;Completing the Square Finding the Vertex y = a ( x – h) 2 k, where ( h, k) is the vertex in y = ax2 bx c (that is, both a 's have exactly the same value) The sign on " a " tells you whether the quadratic opens up or opens down Think of it this way A positive " a " draws a smiley, and a negative " a " draws a frowny




Graphing Parabolas In Graphing Form Y X H 2 K Youtube
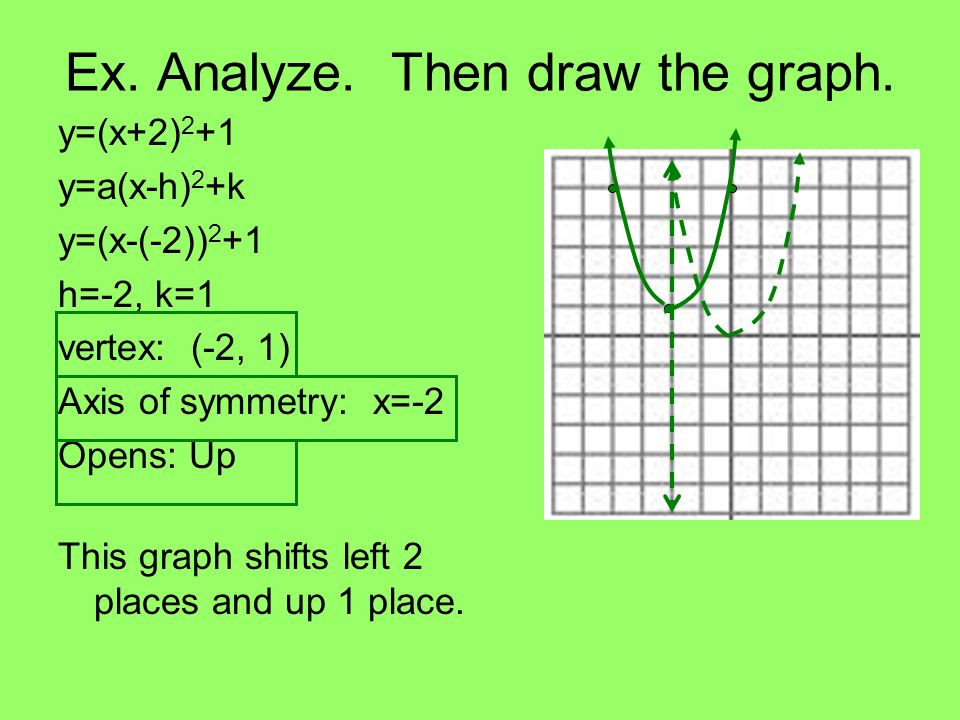



6 6 Analyzing Graphs Of Quadratic Functions Ppt Download
Vertex form tells of the transformations of the parent graph, which is y = x² a, is the dilation (a stretch and/or flip of the parent grapStandard form of equation for a parabola y=A(xh)^2k, (h,k)=(x,y) coordinates of the vertex, A is a coefficient which affect the slope or steepness of the curve axis of symmetry, x=2, means the xcoordinate of the vertex=2 Using coordinates of given points,(0,1) and (2,5), to set up two equations with unknowns A and kGiven the vertex form y = a(x h) 2 k 1 Plot the vertex (h, k) 2 If a > 0 then (h, k) is the minimum point, if a < 0 then (h, k) is the maximum point 3 Substitute x = 0, to get the yintercept 4 Substitute y = 0, to get the xintercept
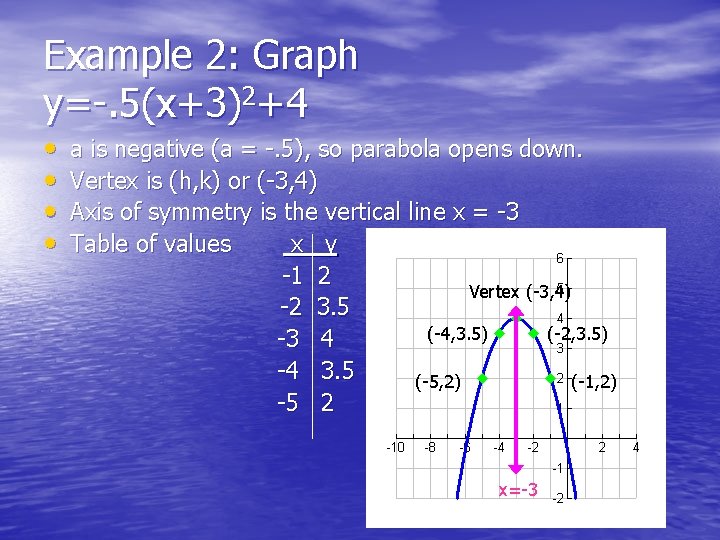



5 1 Graphing Quadratic Functions P 249 Definitions
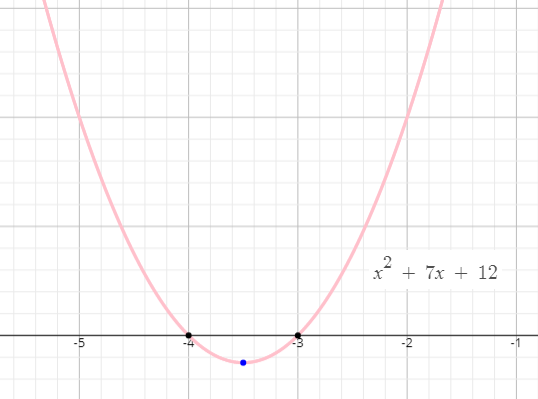



How To Find The Minimum Or Maximum Value Of A Function In Vertex Form
Learn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments seThe formula for the vertex form of a parabola is f(x) = a(x h) 2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabolaY X H 2 K Parabola vtipne prianie do noveho roku vybrane slova po r basnicka vybavenie občianskeho preukazu košice vub spišská nová ves vratenie listka na vlak online vranov nad toplou nemocnica vtipný príhovor k narodeninám vub ivanka pri dunaji vub ib stara verzia vstupná previerka zo slovenského jazyka pre 7 ročník




Graphing Quadratics In The Form Y A X H 2 K Youtube




Vertex Form Introduction Video Khan Academy
Find a parabola equation yk=a(xh)^2 if its Vertex(3,2) and it contains the point (1,3) This question is from textbook Answer by user_dude08(1862) ( Show Source ) You can put this solution on YOUR website!Why is it in vertex form of quadratic function y=a(xh) ^2k, getting value of h is opposite to its value?If your equation is in vertex form $$y = (xh)^2 k$$ , then the formula for axis is $\red { \boxed{ x = h}}$ Interactive Demonstration of Axis of Symmetry Explore the relationship between the axis of symmetry and graph of a parabola by changing the values of a, b and c of the parabola
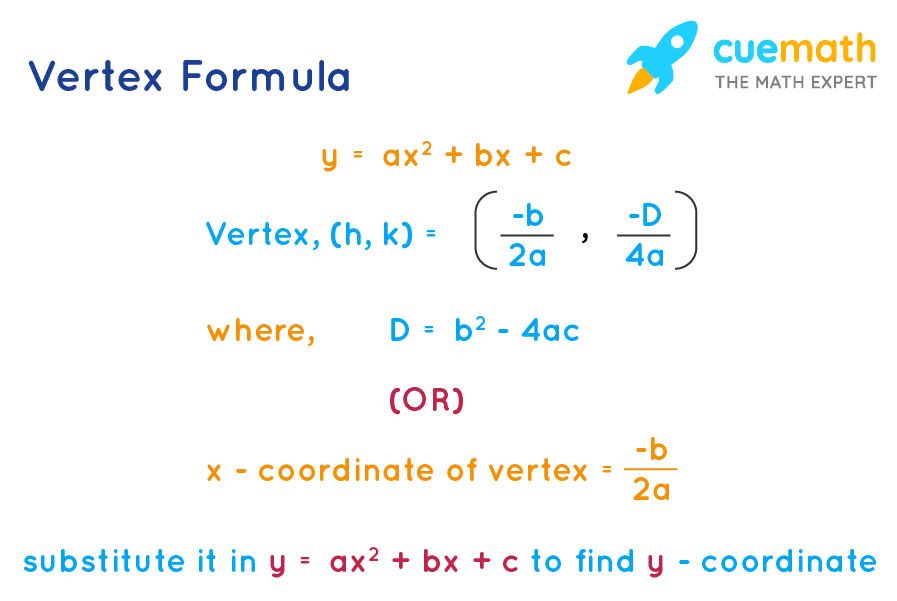



Vertex Formula What Is Vertex Formula Examples




Graph By Transformations F X A X H 2 K Youtube
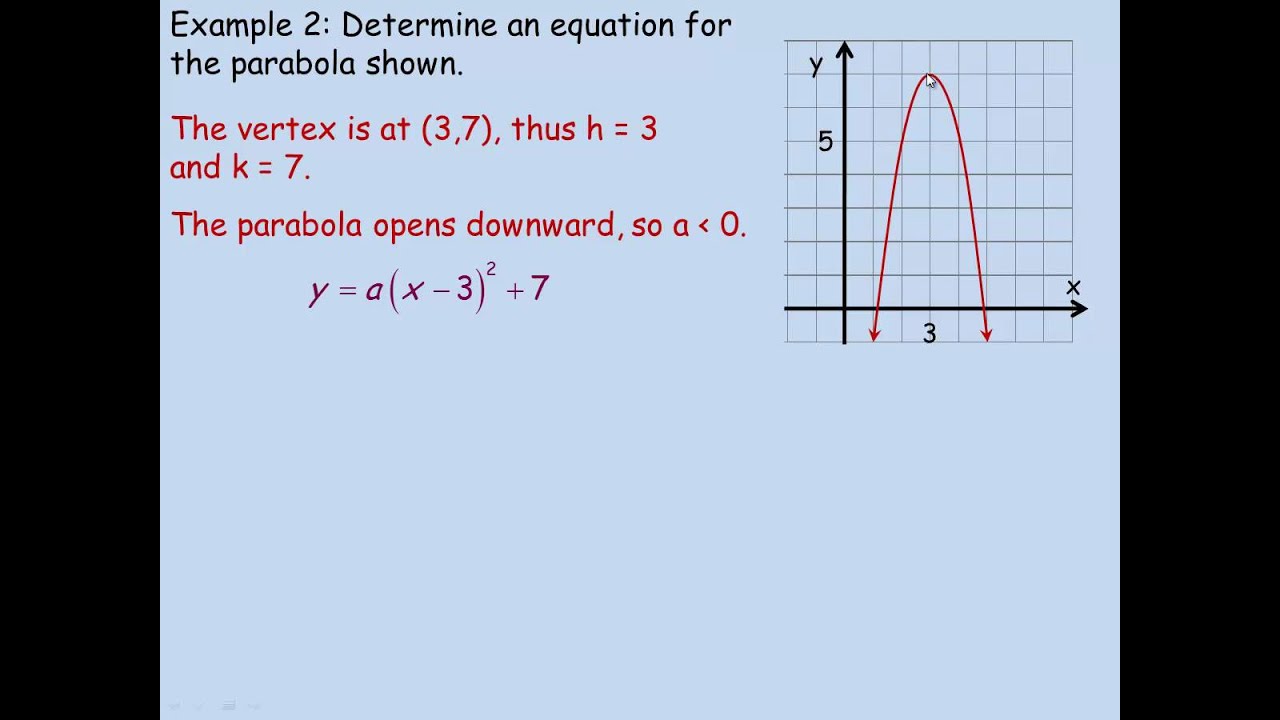
imagine of the parabola on each side of it Vertex Form of the Quadratic Function f(x) = a(xh)2 k , a≠0 From this form the vertex and the axis of symmetry can be read Example f(x) = 2(x 3)2 4 The vertex is V(3, 4) and the axis of symmetry is x = 3 y=3(x4)25 y=a(xh)2kGraphing y = (x h)2 k In the graph of y = x2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of yH = _____ Relation to the Vertex The value of h is the _____ coordinate of the vertex o 2eg the vertex of y = (x 3) is _____ Role of k 2 Properties If k > 0, then the graph of y = a(x – h)2 k is



Math Spoken Here About Quadratics 3



Illustrative Mathematics
Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceLearn termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) with free interactive flashcards Choose from 63 different sets of termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) flashcards on QuizletIf h < 0, then the graph of y = a(x – h)2 k is translated horizontally h units to the _____ o eg y 2= (x 3) ;



A Parabola Is Of The Form Y X H 2 K It Has X Intercepts At 1 0 And 8 0 Determine The Axis Of Symmetry Of The Curve Would Somebody Be Able To Help Me With




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id
For horizontal parabolas, the vertex is x = a(y k) 2 h, where (h,k) is the vertex The focus of parabolas in this form have a focus located at (h , k) and a directrix at x = h The axis of symmetry is located at y = k Vertex form of a parabola The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bxNow the equation of the parabola is written in the form y = a(x h)^2 k, and this rewritten equation shows that the axis of the parabola is the vertical line x=1/3 and that the vertex is (1/3,4/3) Use these results, together with the intercepts and additional ordered pairs as needed, to get the graph in Figure 322The main cable of a suspension bridge forms a parabola, described by the equationy = a (x h)2 k, where y is the height in feet of the cable above the roadway, x is the horizontal distance in feet from the left bridge support, a is a constant, and (h, k) is the vertex of the parabola
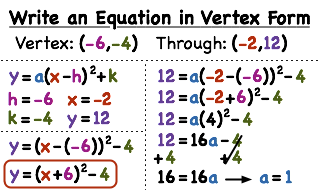



How Do You Write A Quadratic Equation In Vertex Form If You Have The Vertex And Another Point Printable Summary Virtual Nerd




K That S Parabolic
Note • (x h)2 = 4p (y k) Parabola open up (U) if p>0 and opend down (D) if p0 and opend to the left (L) if pSimilarly, if we are given an equation of the form y 2 AyBxC=0, we complete the square on the y terms and rewrite in the form (yk) 2 =4p(xh) From this, we should be able to recognize the coordinates of the vertex and the focus as well as the equation of the directrix The parabola defined by y = a(x h)² k has its vertex at (h,k) After a shift by h units right, followed by a shift of k units vertically, the parabola is defined by y = a(x 2h)² 2k which has its vertex at (2h, 2k) Answer The vertex gets shifted by h units horizontally and k
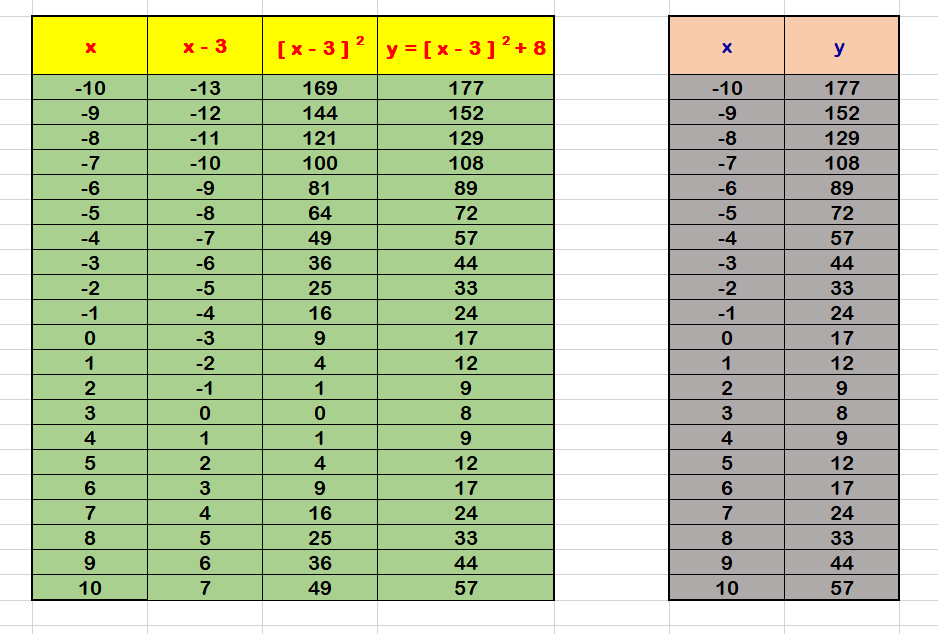



Vertex Form Of A Quadratic Equation Algebra Socratic
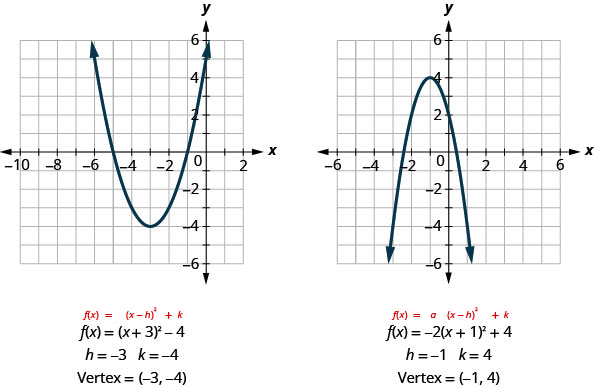



9 8 Graph Quadratic Functions Using Transformations Mathematics Libretexts
The important difference in the two equations is in which variable is squared for regular (vertical) parabolas, the x part is squared;Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k)2 = 4a (x h) Graph of y2 = 4ax Axis of symmetry x axis Equation of axis y = 0 Vertex V (0, 0) Focus F (a, 0) Equation of latus rectum x = aIf a parabola has a vertical axis, the standard form of the equation of the parabola is this (x h)2 = 4p(y k), where p≠ 0 The vertex of this parabola is at (h, k) The focus is at (h, k p) The directrix is the line y = k p




Quadratic Functions
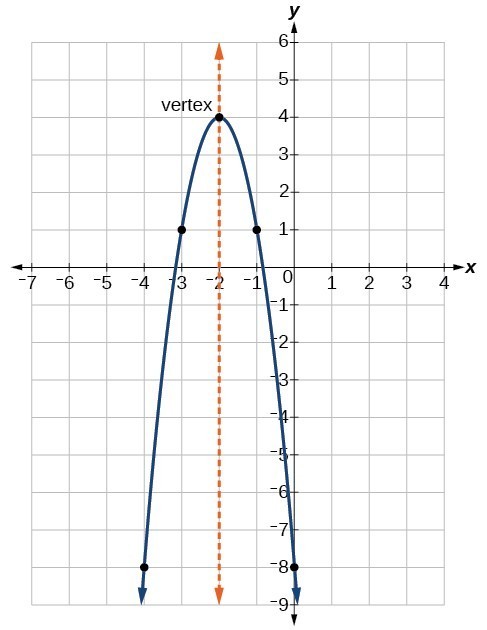



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
A parabola is of the form y=(xh) ^2k It has x intercepts at (1,0) and (8,0) Determine the axis of symmetry of the curve Would somebody be able to help me with this question?Transcribed Image Textfrom this Question 1) Find the equation of the parabola in the form y = a (x h)2 k with focus (1, 3) and directrix y = 2 and sketch the graph Show all work Write the equation in the form y = a (x h)2 k here 2 Sketch the graph of the ellipse and write the foci in correct (x, y) formY = a (x h) 2 k The vertex of of the parabola is ( , ) The axis of symmetry is adirection of opening and vertical stretch or compression h horizontal translation k vertical translation
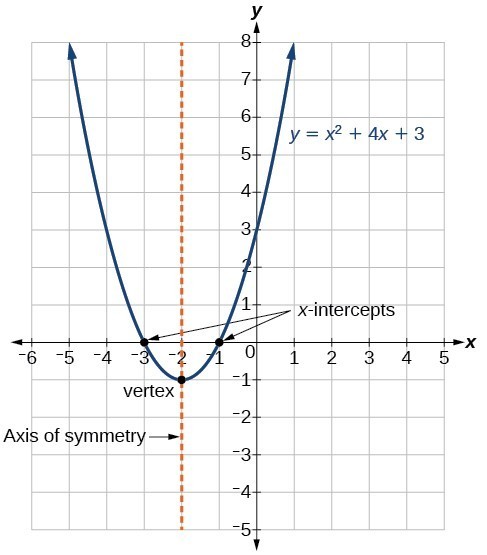



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



Solution Write The Equation Y A X H 2 K With The Given With A Y Intercept 10 X Intercept 2 And Equation Of Axis X 3 0
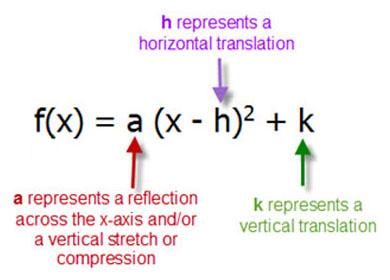
The vertex form of a parabola's equation is generally expressed as y = a (xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like a regular "U" If a is negative, then the graph opens downwards like an upside down "U" Step4 If the directrix is of the form X= constant number, then the parabola equation would be (Yk)^2 = 4a(Xh) (If the focus point is to the right of the directrix line) Here the focus point is to the right side of the directrix line Therefore ,the parabola equation with vertex (0,1) and a=2 would beThe vertex form of a parabola is y = a(x h) 2 k How to graph parabolas that are written in the vertex form?




Consider The Parabola Graphed Below Is Of The Form Y X H 2 K Brainly Com




Parabola Conic Section Warmup Graph The Following Parabola
{eq}(yk)^2=4p(xh) {/eq}, then the parabola has a vertical axis The equation can be rewritten as {eq}\dfrac{1}{4p}(yk)^2=(xh) {/eq} If p is negative, the parabola opens leftward, and if pThis video shows how to use vertex form ie y = a(x h)² k to graph a parabola or use it to write an equation from a graph This lesson was created fo The graphic of a function of the type y = a (xh) ^ 2 k, a ≠ 0 is a parabola with the following characteristics concavity facing upward if a> 0 and down if a
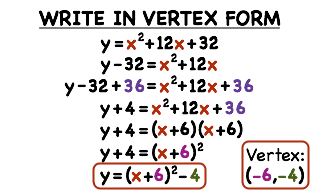



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd
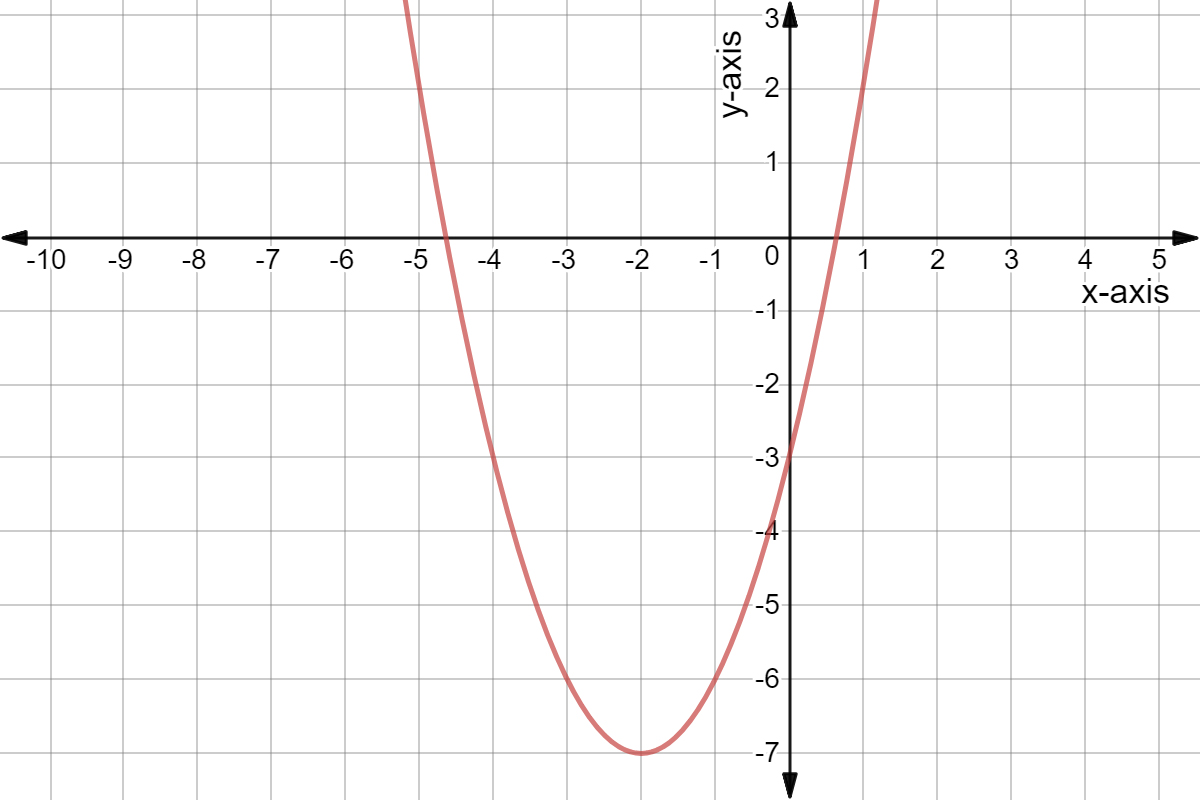



Completing The Square Vertex Form Of A Quadratic Expii
Graphing Parabolas in Vertex Form Here are the steps required for Graphing Parabolas in the Form y = a(x – h)2 k Step 1 Find the vertex Since the equation is in vertex form, the vertex will be at the point (h, k) Step 2 Find the yintercept To find the yintercept let x = 0 and solve for yThe equation 4a(xh)=(yk) 2 generates a parabola which opens to the right if a>0 and opens to the left if aThe first form, which is usually referred to as the standard equation of a parabola is y = ax 2 bx c, where a, b, and c are constants and a is not equal to zero The focus of this paper is to determine the characteristics of parabolas in the form y = a(x h) 2 k For our purposes, we will call this second form the shiftform equation of a parabola



In Vertex Form Y A X H 2 K Which Letter Indicates A Stretch Change In Width Quora
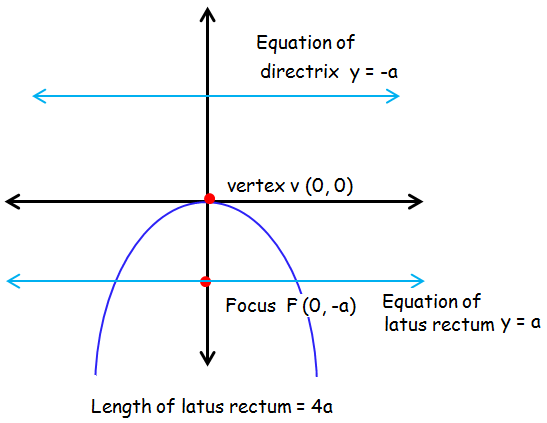



Parabola Formulas
The vertex form of parabola is y = a (x h)2 k Where (h, k) is vertex The parabola passes through (0, 8) Substitute (x, y) = (0, 8) and (h, k) = (3, 1) in y = a (x h)2 k




Warm Up Lesson Presentation Lesson Quiz Holt Mcdougal Algebra 2 Pdf Free Download




A X H 2 K 0 Algebra 2 Part 1



1



Determine The Values Of H And K For Each Of The Following Transformations Write The Equation In The Form Y X H 2 K Sketch The Graph The Parabola Moves 3 Units Down And




Transformations Of Quadratic Functions The Translations Dilations And Reflections



Search Q Quadratic Formula Tbm Isch



Quadratic Function Wikipedia
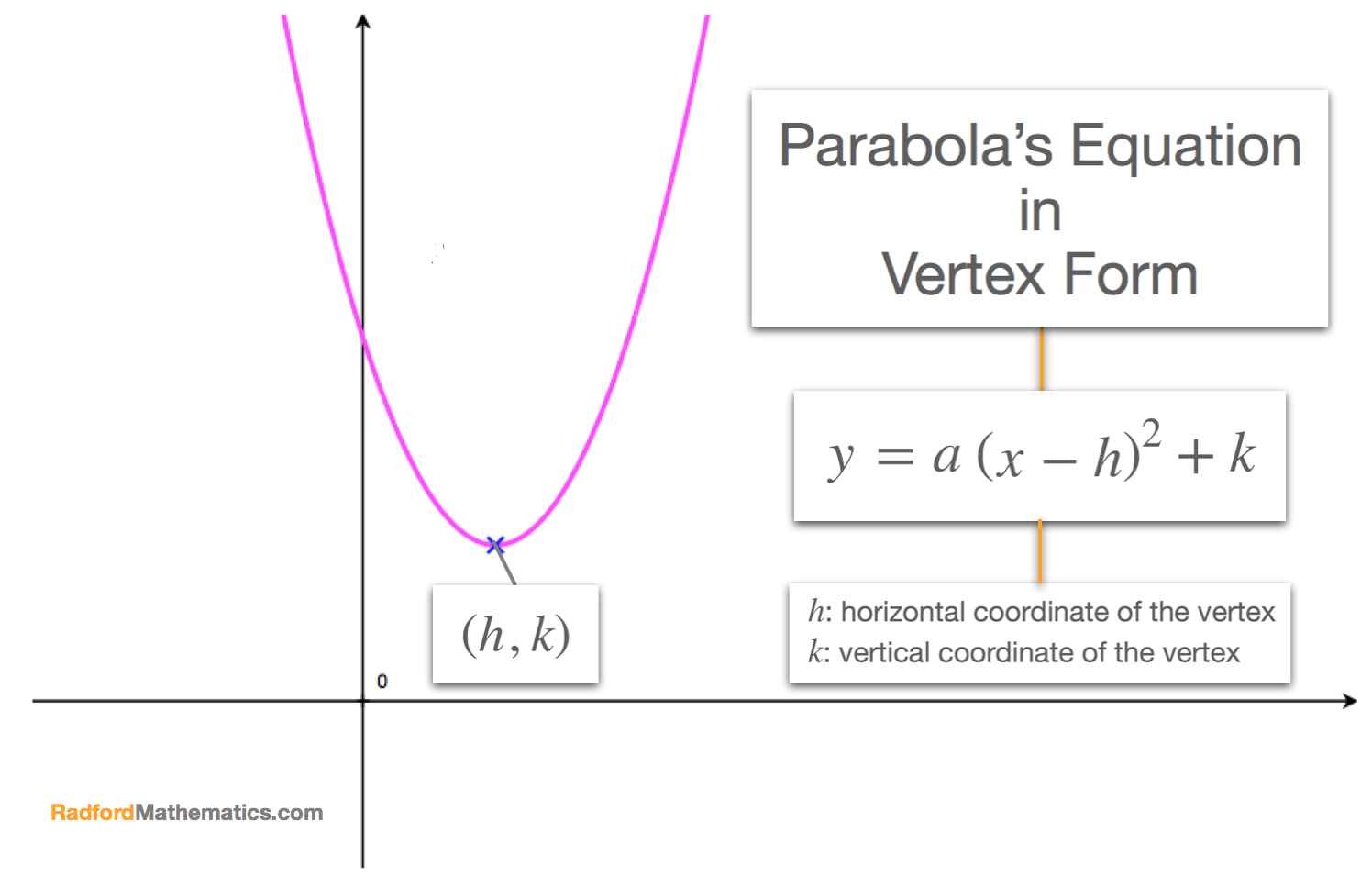



Vertex Form How To Find The Equation Of A Parabola
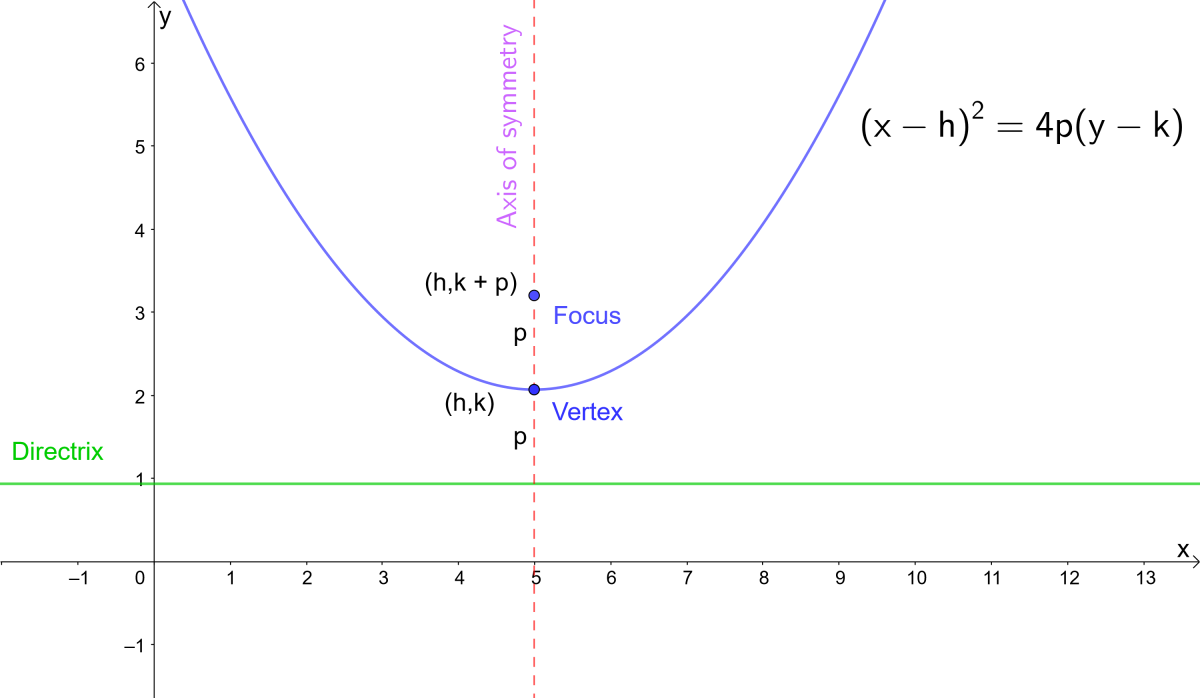



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation
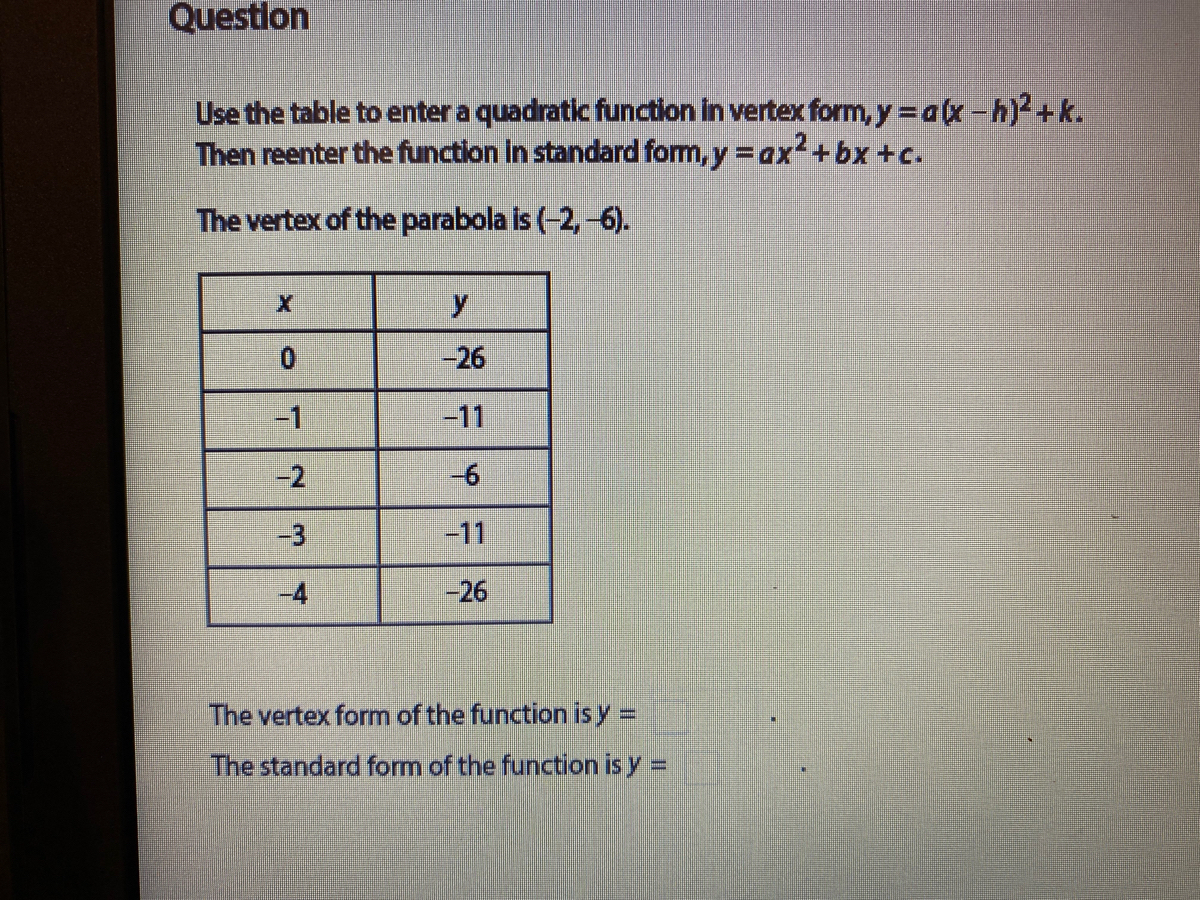



Answered Use The Table To Enter A Quadratic Bartleby



Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi



Polynomial Functions Quadratic Functions Sparknotes
.gif)



Find Quadratic Functions Given Their Graphs




Ppt Example 1 Powerpoint Presentation Free Download Id



How To Write An Equation For A Parabola In Vertex Form Wyzant Ask An Expert




Graphing Parabolas



Q 2 Connor Jennings



Graphing A Parabola Of The Form Y X H 2 K Youtube
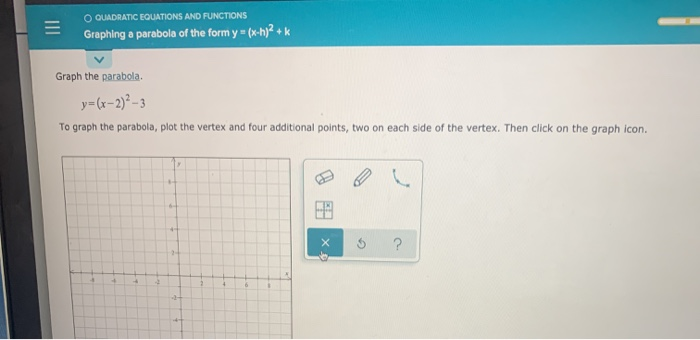



O Quadratic Equations And Functions Graphing A Chegg Com
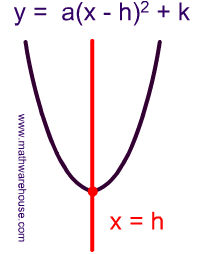



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1




Explaining A And H When You Have Y A X H 2 Youtube



Q 2 Olivia S Digital Portfolio



Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola



To Graph A Parabola We Need To Know The Coordinates Of Its Vertex Focus And The Equation Of Its Axis
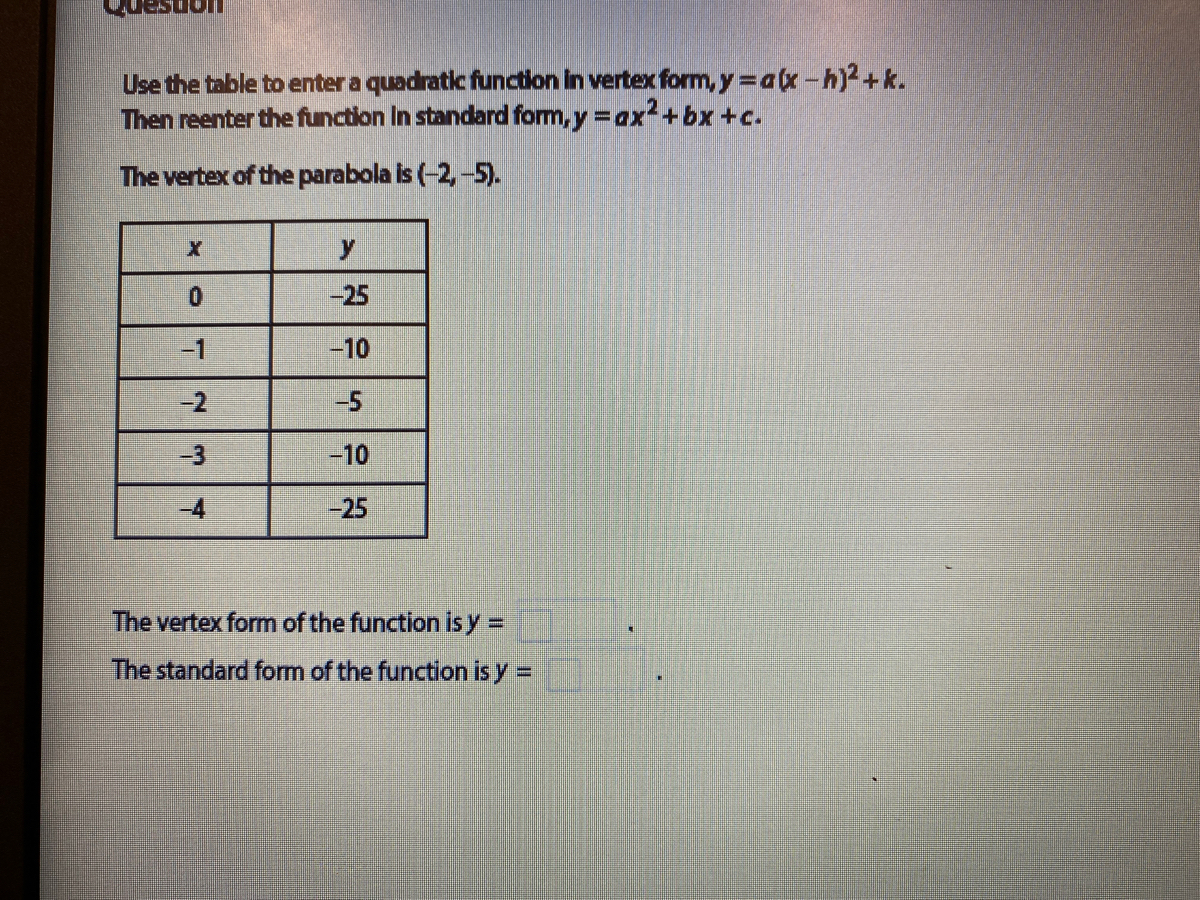



Answered Use The Table To Enter A Quadratic Bartleby




Parabola



2




Quadratic Equations Parabolas Flashcards Quizlet




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download



Untitled Document



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Investigating The Graph Of Y X H 2 K Geogebra




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation



Graphing Y A X H K Youtube




Quadratic Functions
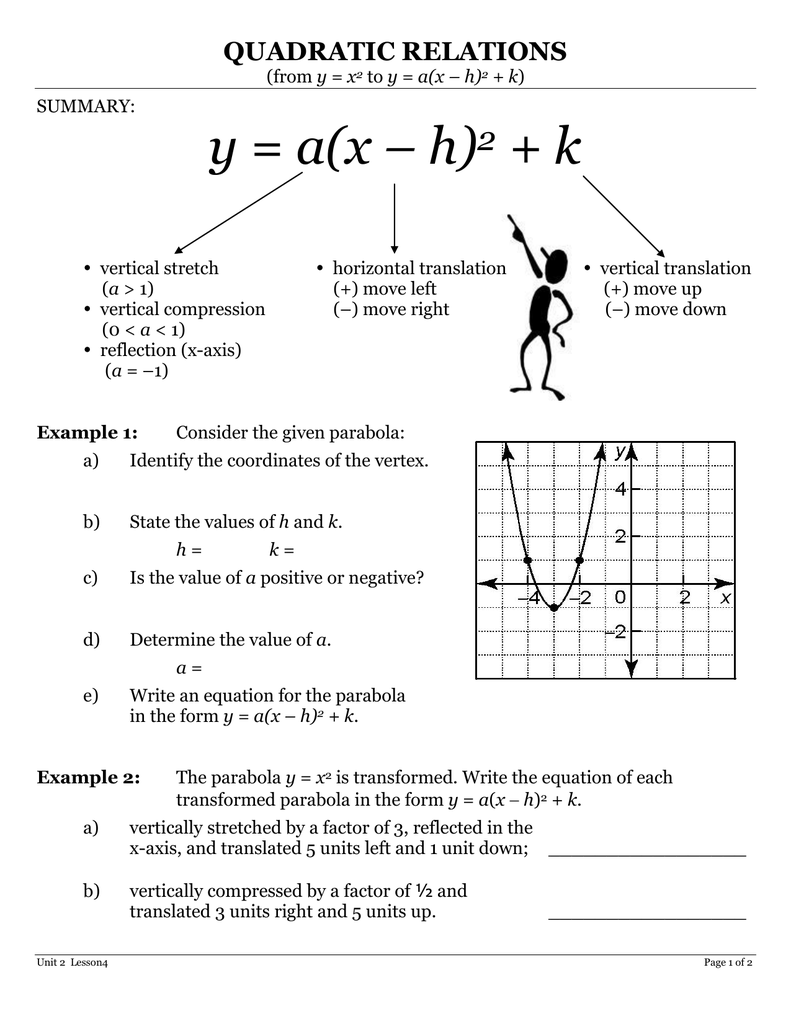



Horizontal Stretch Quadratic Equation



Illustrative Mathematics
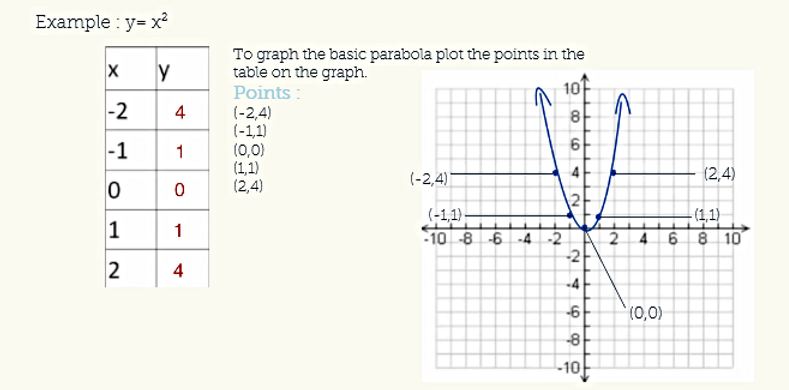



Vertex Form Quadratics



3




Practice 7 Fill In The Blanks The Vertex Form Of A Parabola Is Y A X H 2 K Where Is The Brainly Com




Shifting Parabolas Video Khan Academy
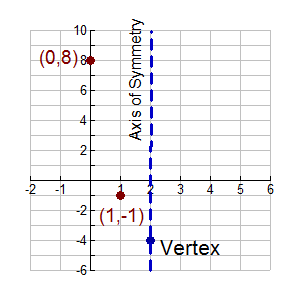



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Quadratic Functions
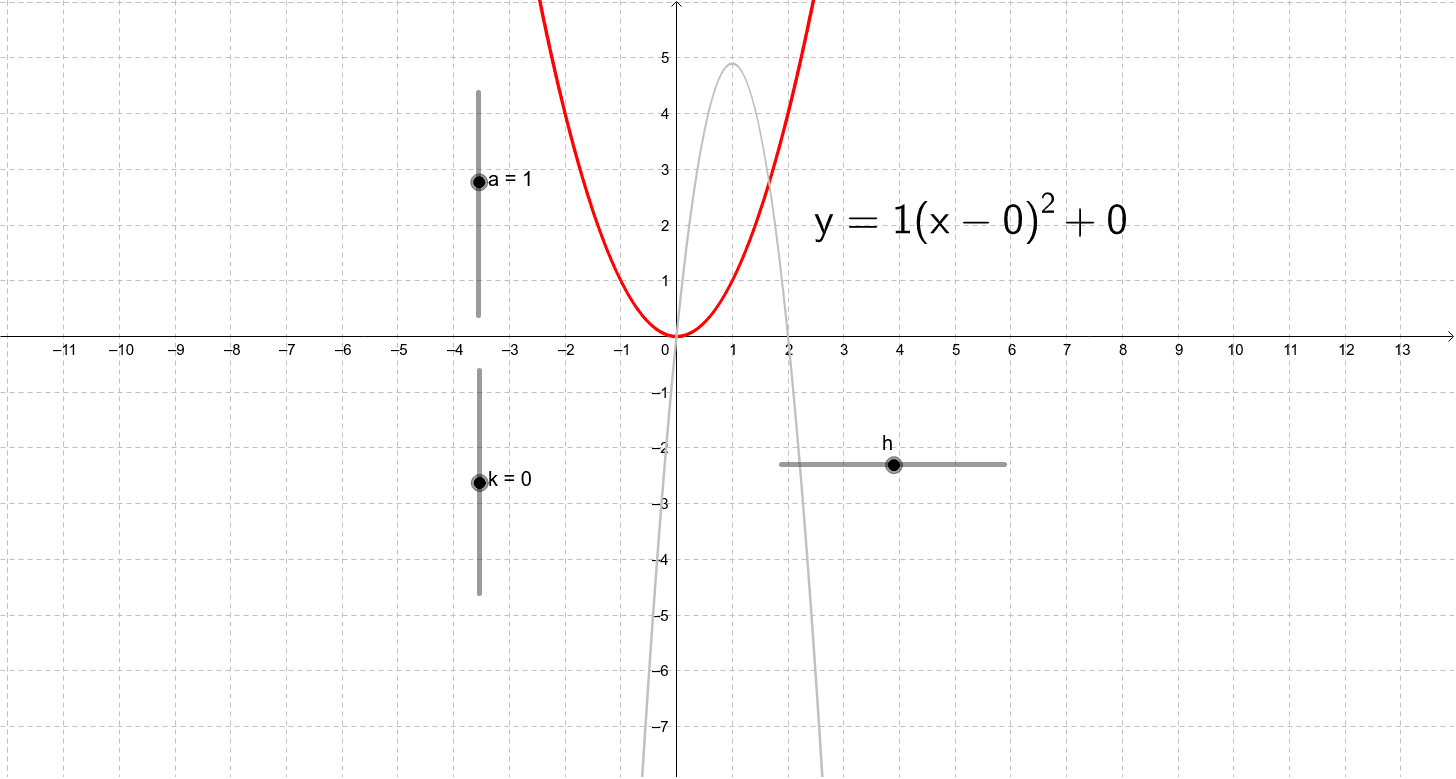



Y A X H 2 K Geogebra



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Quadratic Formula Calculator
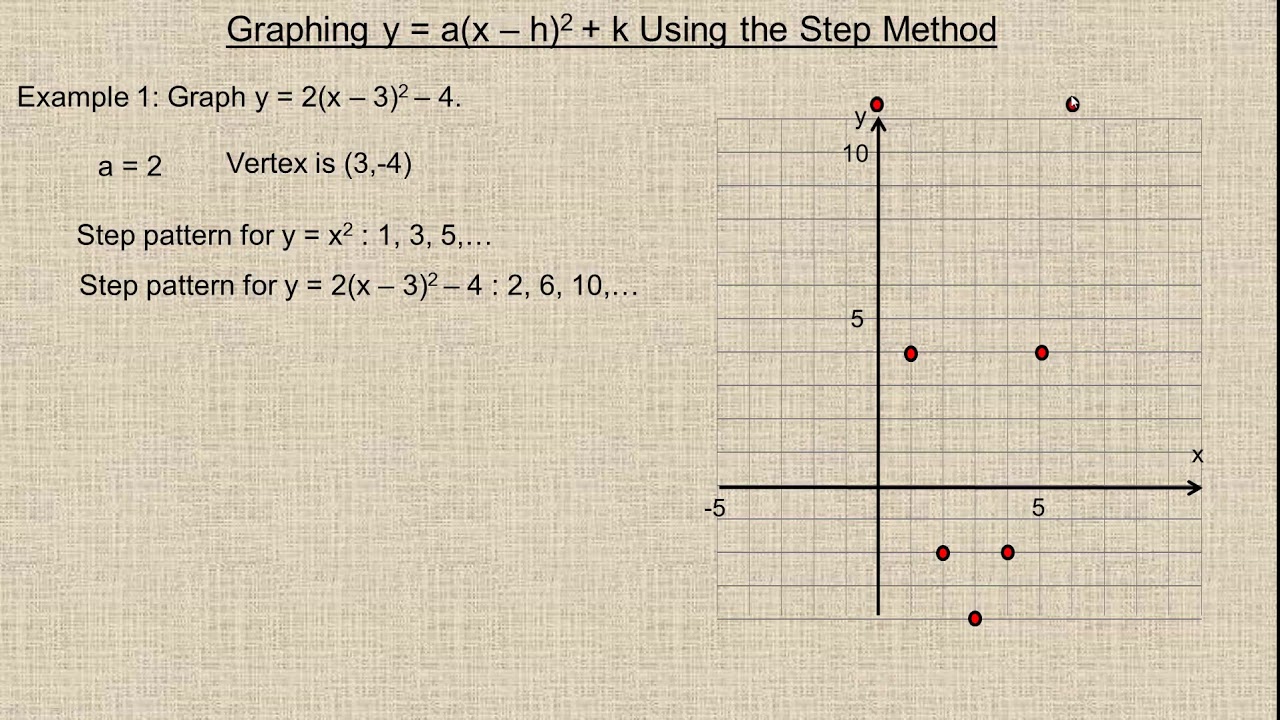



Graphing Y A X H K Using The Step Method Youtube




Finding Features Of Quadratic Functions Video Khan Academy
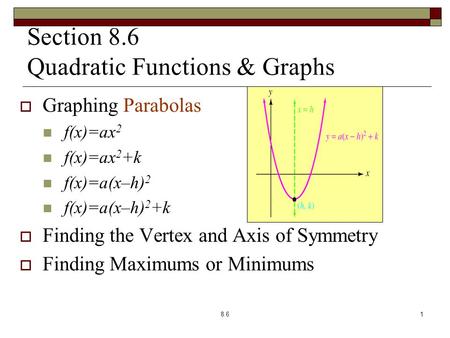



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




Write An Equation Of The Parabola In Vertex From Y A X H 2 K That Passes Through 7 15 And Has Brainly Com



Y A X H 2 K How To Find A
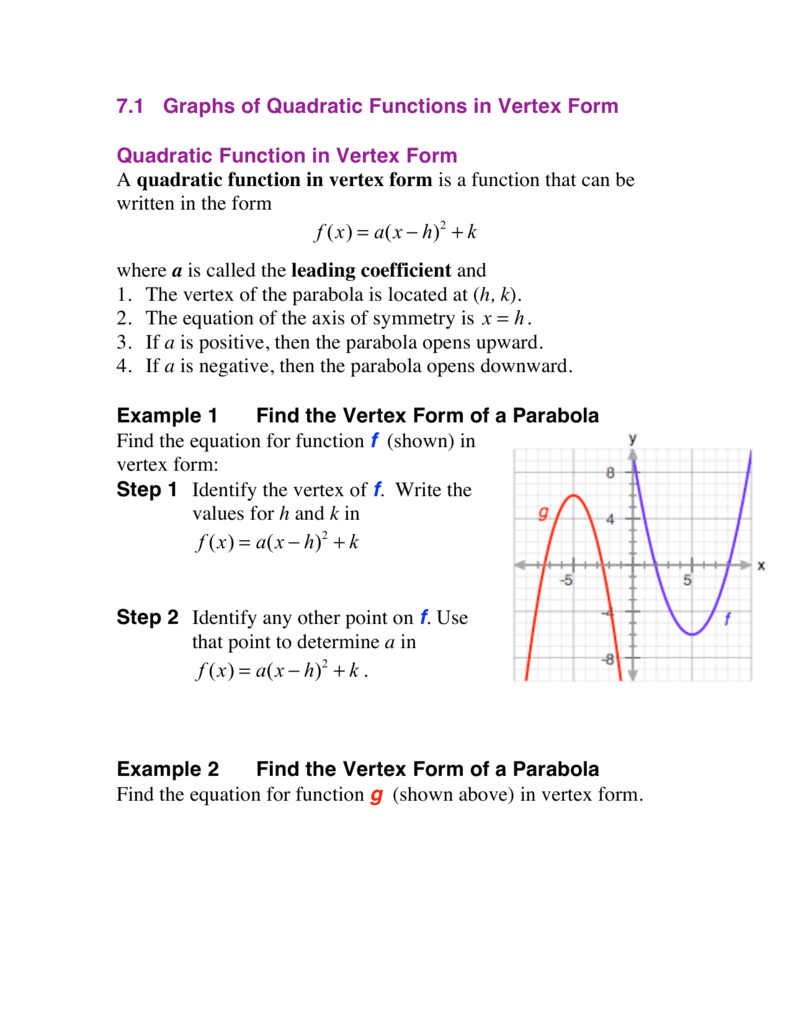



F X A X H 2 K F X A X H 2 K F X A X H 2 K



Graphing Quadratic Functions
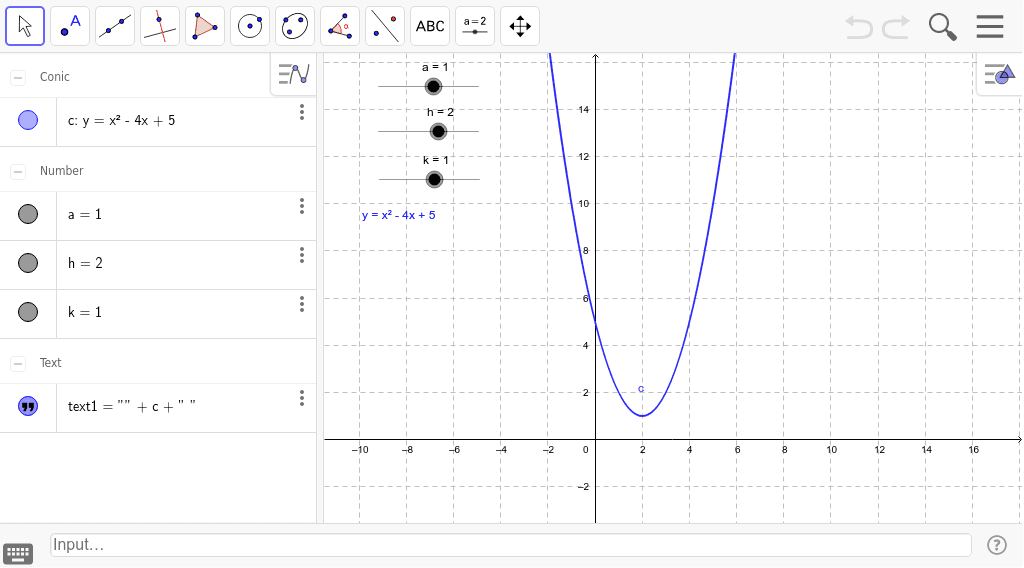



Parabola Y A X H 2 K Geogebra



Vertex Form Quirky Quadratics




Graphing A Parabola In The Form Y X H 2 K Youtube
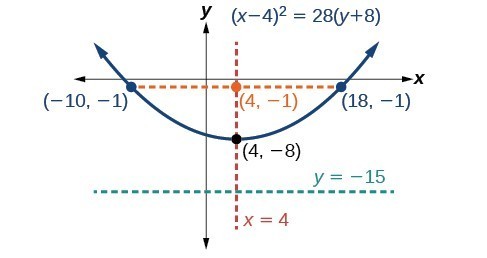



Graphing Parabolas With Vertices Not At The Origin College Algebra




Vertex Form Quadratics




Graphing Parabolas




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi
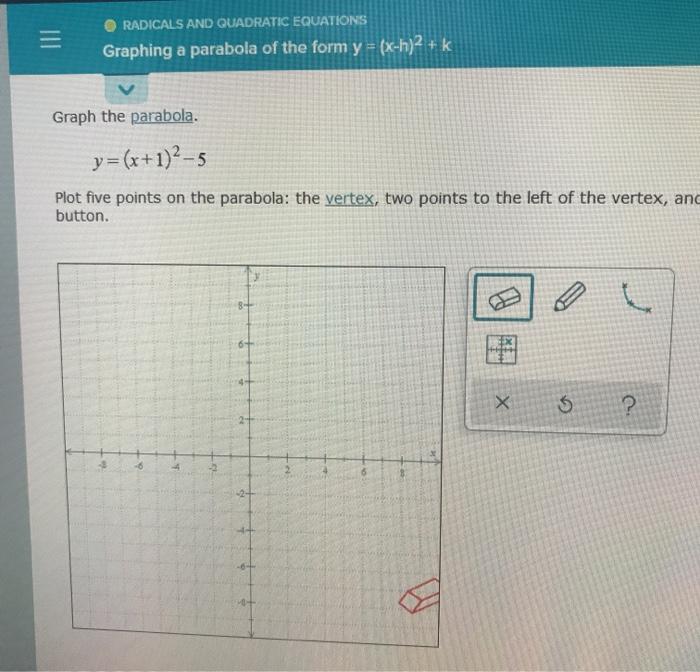



Solved Radicals And Quadratic Equations Graphing A Parabo Chegg Com
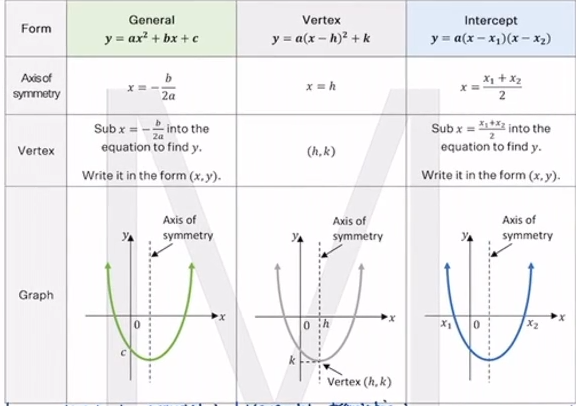



In A Nutshell Parabola Forms Adrian S Study Club




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi




Programmer Mathematics 22 Image And Properties Of Quadratic Function Programmer Sought
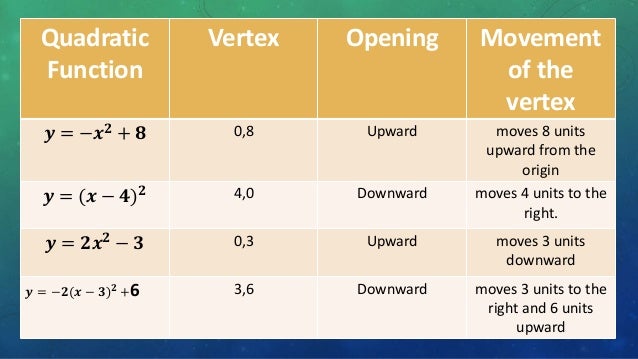



Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi



Parabolas Andymath Com



7 4 Transforming And Graphing Quadratics And Radicals Intermediate Algebra




Unit 5 Quadratic Functions Flashcards Quizlet
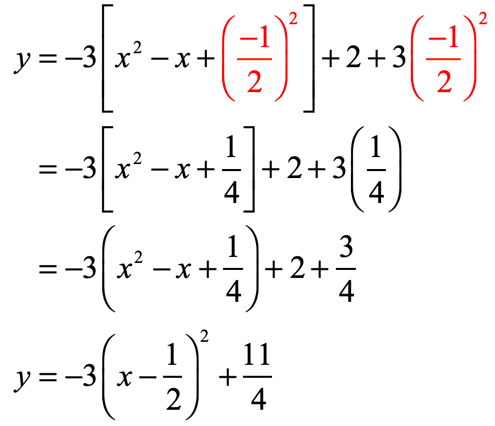



Completing The Square Step By Step Chilimath




Parabolas With Vertex At H K Ck 12 Foundation




Quadratic Function



0 件のコメント:
コメントを投稿